Квадрат высоты проведенной к гипотенузе равен произведению величин отрезков на которые он делит гипотенузу.
H^2 = 9 × 16 = 144
Теперь рассмотрим два треугольника, полученные при делении высотой исходного на два. Они оба прямоугольные, одним катетом является высота H, а вторыми катетами являются отрезки по 9см. и 16см.
Дано: AM ║DH ║BP, A,B,D ∈ α, D ∈ AB, MH = 12, HP = 8, BD = 14
Найти: AB - ?
Решение: Через прямые AM, DH, BP можно провести одну и ту же плоскость и только одну по теореме, тогда плоскость проведенная через параллельный прямые AM, DH, BP пересекает плоскость по прямой по следствию из аксиом стереометрии. То ест точки A, D, B - лежат на одной прямой и в одной плоскости α (A,B,D ∈ α по условию).Так как по условию AM ║DH и DH ║BP то MADH и BDHP - трапеции по определению, так же эти трапеции лежат на параллельны прямых которые пересекают плоскость α в точках которые лежат на одной прямой тогда по теореме MADH и BDHP - подобные трапеции, следовательно ⇒ .
Відповідь:
15 см. 20 см. 25 см.
Пояснення:
Квадрат высоты проведенной к гипотенузе равен произведению величин отрезков на которые он делит гипотенузу.
H^2 = 9 × 16 = 144
Теперь рассмотрим два треугольника, полученные при делении высотой исходного на два. Они оба прямоугольные, одним катетом является высота H, а вторыми катетами являются отрезки по 9см. и 16см.
Катеты исходного треугольника равны:
sqrt ( 144 + 81 ) = sqrt ( 225 ) = 15 см.
sqrt ( 144 + 256 ) = sqrt ( 400 ) = 20 см.
Гипотенуза равна:
9 + 16 = 25 см.
Объяснение:
Дано: AM ║DH ║BP, A,B,D ∈ α, D ∈ AB, MH = 12, HP = 8, BD = 14
Найти: AB - ?
Решение: Через прямые AM, DH, BP можно провести одну и ту же плоскость и только одну по теореме, тогда плоскость проведенная через параллельный прямые AM, DH, BP пересекает плоскость по прямой по следствию из аксиом стереометрии. То ест точки A, D, B - лежат на одной прямой и в одной плоскости α (A,B,D ∈ α по условию).Так как по условию AM ║DH и DH ║BP то MADH и BDHP - трапеции по определению, так же эти трапеции лежат на параллельны прямых которые пересекают плоскость α в точках которые лежат на одной прямой тогда по теореме MADH и BDHP - подобные трапеции, следовательно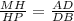 ⇒
⇒ 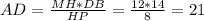 .
.
AB = AD + DB = 14 + 21 = 35.