Найти точку пересечения медиан треугольника АВС, где A(1; 4; -3), B(2; -1; 9), C(0; 3; -6).

Показать ответ

Ответ:

ByGaTiVlAdLeN

16.04.2022 14:21

1.Сумма углов = 180°
180°-40°=140° - сумма двух других углов,
140°-16°:2°+=62° - третий угол,
и 62°+16°=78°- второй уголответ: 40°, 78°, 62°

2.есть 2 случая:
Углы при основании равны 70° т. к. 180° - 110° = 70°, а углы при основании равнобедренного треугольника равны, а угол при вершине равен 40°, т. к. 180° - ( 70° + 70° ) = 40°
Или если внешний угол смежный с углом противолежащим основанию. тогда равные углы равны по 55°, а другой угол 70°

3.
ΔADC - прямоугольный, в нём <ACD = 60° т.к. ΔАВС - равносторонний <CAD = 30°, значит, катет CD, лежащий против угла в 30° равен половине гипотенузы АС х - CD 2x - AC Уравнение х + 2х + 10 = 70 3х = 60 х = 20 СD = 20 см AC = 40 см это сторона равностороннего ΔАВС Р = 3 * АС Р = 40 * 3 = 120 см ответ: Р = 120 см

0,0(0 оценок)

Ответ:

Kulimshina

29.01.2022 16:12

Продолжим касательные до их пересечения в т.Р.

ОА⊥АС и О1С⊥АС ( радиусы, проведенные в точку касания.

Из т.О проведем параллельно АС прямую до пересечения с СО1 в т.Н.

Четырехугольник АОНС - прямоугольник. СН=АО=r=12 ⇒

О1Н=20-12=8

⊿ ОНО1 - прямоугольный. ОО1=12+20=32.

По т.Пифагора

ОН=√(OO1²-O1H²)=√(32²-8²)=√960=8√15

cos∠HOO1=OH:OO1=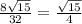 $\frac{8 \sqrt{15} }{32} = \frac{ \sqrt{15} }{4}$

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.⇒

РС=РD, PA=PB ⇒ BD=AC=8√15

∆ СРD равнобедренный, ∆ РАВ равнобедренный ⇒

биссектриса АО1 перпендикулярна АВ и СD

∠СРО1=∠DPO1

Расстояние между АВ и СD - длина общего между ними перпендикуляра.

Проведем ВМ || РО1

ВМ⊥АВ и ВМ⊥СD.

∆ ВМD прямоугольный. ∠МВD=∠O1PD

ВМ=BD•cosO1PD=8√15•√15:4=30