"Во французской стороне, на чужой планете" - я уверена, многие из нас не только слышали эти слова, но и знают продолжение или даже пели когда-то. Песенка хорошо известна российскому студенчеству, хотя пришла к нам из далекой средневековой Европы. Мне кажется, я знала ее, сколько себя помню, и меня всегда интересовало, кто ее автор. Каково же было мое удивление, когда еще в школе я столкнулась с ней в разделе про средневековые университеты и тогда впервые услышала странное слово "ваганты"(иногда их еще называют "голиардами").
Ваганты - это бродячие школяры (студенты, иногда клирики). Пик развития движения вагантов приходился на XII - первую половину XIII вв, хотя началось все раньше - в XI в с созданием и развитием университетов. Университет - совершенно новое явление средневековья - это было "объединение, спаянное взаимной клятвой". Ново было то, что основой этого объединения был интеллектуальный труд. Ново было свободомыслие и равенство. Движение вагантов было тоже новым, но как будет рассказано ниже, оно дало начало многим процессам того и нашего времени.
Ваганты были студентами (так же, как я сейчас), они учились и бродяжничали, они жили. Естественно, что их жизнь очень интересна нам теперешним: мы хотим найти отличия и сходства, понять насколько и что изменилось за эти века. Сквозь века мы слышим и видим родственные души, и мы протягиваем им руки, пытаюсь не только вытащить их тени в наш мир, но и сделать их живыми и яркими, реконструировать тот мир. Их поэзия, их жизнь, их образы - все это создает неповторимое и уникальное пространство -
21.04.2018 11:49
thumb_up 37
Знаете ответ? Поделитесь им!

Гость ?
Как написать хороший ответ?
Электронная почта
Пароль
◢
Мой ответ
add_circle
Изображение
Максимальный размер загружаемых файлов 10 Мб
ОТВЕТИТЬ
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе История.
Трудности с домашними заданиями? Не стесняйтесь попросить о смело задавайте вопросы!
История — область знаний, а также гуманитарная наука, занимающаяся изучением человека в
Новые вопросы
{XyLi}GaN
История
Katysha
История
С текста параграфа и дополнительных источников информации составьте рассказ об одном из собы...
lidapogodina48
История
Как сделать эту работу ?
arinatsip99
История
lagerel
История
Составьте таблицу по теме :Мир художественной культуры просвещения(направление, дата, деятель, дости...
asdtry5fggg
История
Усуни Кангюи скиньте лист
harukscat753
История
к сообщению сделать цель, задачи и вывод. Храмы строят по-разному. Ведь храм го...
1) Через пересекающиеся прямые можно провести плоскость. ⇒ а и b лежат в одной плоскости. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. А1В1||А2В2.
∆ А1КВ1~А2КВ2, т.к. углы при пересечении параллельных оснований секущими а и b равны, и угол К - общий.
Из подобия следует: КВ1:КВ2=А1В1:А2В2=3/4
Примем В1В2=х, тогда КВ2=14+х
14:(14+х)=3:4
56=42+3х ⇒ ⇒
см
2) Медианы треугольника пересекаются, параллельны плоскости альфа, следовательно, плоскость треугольника, в которой они лежат, параллельна плоскости альфа.
СЕ и ВF параллельны ( дано), следовательно, через них можно провести плоскость, притом только одну.
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.⇒ СВ||EF.
Четырехугольник, у которого противоположные стороны попарно параллельны, является параллелограммом, ч.т.д.
3) Все грани параллелепипеда ABCDA1B1C1D1 - квадраты со стороной a.⇒ этот параллелепипед - куб.
DA1В1С - прямоугольник, т.к. по т. о 3-х перпендикулярах диагонали А1D и В1С параллельных граней перпендикулярны ребрам А1В1 и DC . Проведем через середины АD и ВC прямые КМ и ОН параллельно А1D и В1C, соединим К и О, М и Н. Пересекающиеся КО и КА параллельны пересекающимся АА1 и АD. ⇒
Плоскость сечения МКОН параллельна плоскости DA1B1C ⇒ . Стороны сечения КМНО пересекают ребра АА1, ВВ1, ВС и AD в их середине. КМНО - прямоугольник.
В параллельных гранях диагонали А1D=B1C=a:sin45°=a√2
КМ и ОН –– средние линии ∆ АА1D и ВВ1С соответственно и равны половине А1D- равны
"Во французской стороне, на чужой планете" - я уверена, многие из нас не только слышали эти слова, но и знают продолжение или даже пели когда-то. Песенка хорошо известна российскому студенчеству, хотя пришла к нам из далекой средневековой Европы. Мне кажется, я знала ее, сколько себя помню, и меня всегда интересовало, кто ее автор. Каково же было мое удивление, когда еще в школе я столкнулась с ней в разделе про средневековые университеты и тогда впервые услышала странное слово "ваганты"(иногда их еще называют "голиардами").
Ваганты - это бродячие школяры (студенты, иногда клирики). Пик развития движения вагантов приходился на XII - первую половину XIII вв, хотя началось все раньше - в XI в с созданием и развитием университетов. Университет - совершенно новое явление средневековья - это было "объединение, спаянное взаимной клятвой". Ново было то, что основой этого объединения был интеллектуальный труд. Ново было свободомыслие и равенство. Движение вагантов было тоже новым, но как будет рассказано ниже, оно дало начало многим процессам того и нашего времени.
Ваганты были студентами (так же, как я сейчас), они учились и бродяжничали, они жили. Естественно, что их жизнь очень интересна нам теперешним: мы хотим найти отличия и сходства, понять насколько и что изменилось за эти века. Сквозь века мы слышим и видим родственные души, и мы протягиваем им руки, пытаюсь не только вытащить их тени в наш мир, но и сделать их живыми и яркими, реконструировать тот мир. Их поэзия, их жизнь, их образы - все это создает неповторимое и уникальное пространство -
21.04.2018 11:49
thumb_up 37
Знаете ответ? Поделитесь им!

Гость ?
Как написать хороший ответ?
Электронная почта
Пароль
◢
Мой ответ
add_circle
Изображение
Максимальный размер загружаемых файлов 10 Мб
ОТВЕТИТЬ
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе История.
Трудности с домашними заданиями? Не стесняйтесь попросить о смело задавайте вопросы!
История — область знаний, а также гуманитарная наука, занимающаяся изучением человека в
Новые вопросы
{XyLi}GaN
История
Katysha
История
С текста параграфа и дополнительных источников информации составьте рассказ об одном из собы...
lidapogodina48
История
Как сделать эту работу ?
arinatsip99
История
lagerel
История
Составьте таблицу по теме :Мир художественной культуры просвещения(направление, дата, деятель, дости...
asdtry5fggg
История
Усуни Кангюи скиньте лист
harukscat753
История
к сообщению сделать цель, задачи и вывод. Храмы строят по-разному. Ведь храм го...
prishel
История
Подскажите три проблемы исторического знания
О нас
О проекте
Обратная связь
Вопросы
Правила
Политика конфиденциальности
© Online-Otvet.ru, 2012-2020
Этот сайт использует cookies Политика Cookies. Вы можете указать условия хранения и доступ к cookies в своем браузере.
1) Через пересекающиеся прямые можно провести плоскость. ⇒ а и b лежат в одной плоскости. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. А1В1||А2В2.
∆ А1КВ1~А2КВ2, т.к. углы при пересечении параллельных оснований секущими а и b равны, и угол К - общий.
Из подобия следует: КВ1:КВ2=А1В1:А2В2=3/4
Примем В1В2=х, тогда КВ2=14+х
14:(14+х)=3:4
56=42+3х ⇒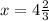 ⇒
⇒
2) Медианы треугольника пересекаются, параллельны плоскости альфа, следовательно, плоскость треугольника, в которой они лежат, параллельна плоскости альфа.
СЕ и ВF параллельны ( дано), следовательно, через них можно провести плоскость, притом только одну.
Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.⇒ СВ||EF.
Четырехугольник, у которого противоположные стороны попарно параллельны, является параллелограммом, ч.т.д.
3) Все грани параллелепипеда ABCDA1B1C1D1 - квадраты со стороной a.⇒ этот параллелепипед - куб.
DA1В1С - прямоугольник, т.к. по т. о 3-х перпендикулярах диагонали А1D и В1С параллельных граней перпендикулярны ребрам А1В1 и DC . Проведем через середины АD и ВC прямые КМ и ОН параллельно А1D и В1C, соединим К и О, М и Н. Пересекающиеся КО и КА параллельны пересекающимся АА1 и АD. ⇒
Плоскость сечения МКОН параллельна плоскости DA1B1C ⇒ . Стороны сечения КМНО пересекают ребра АА1, ВВ1, ВС и AD в их середине. КМНО - прямоугольник.
В параллельных гранях диагонали А1D=B1C=a:sin45°=a√2
КМ и ОН –– средние линии ∆ АА1D и ВВ1С соответственно и равны половине А1D- равны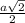
КО=МН=АВ=а
Р (КМНО=2(МН+КМ)=2a+2•(a√2/2)=a•(2+√2)