Так как АВ = DB (по условию), то ΔАВD - равнобедренный (по определению равнобедренного треугольника). Причём AD - это его основание (так как АВ и DB - боковые стороны).
В равнобедренном треугольнике высота, проведённая к его основанию, является также его биссектрисой.
Дано :
ΔАВD, АВ = DB.
ВС - высота (ВС⊥AD).
∠ABD = 58°.
Найти :
∠АВС = ?
Так как АВ = DB (по условию), то ΔАВD - равнобедренный (по определению равнобедренного треугольника). Причём AD - это его основание (так как АВ и DB - боковые стороны).
В равнобедренном треугольнике высота, проведённая к его основанию, является также его биссектрисой.Следовательно, отрезок ВС - биссектриса ∠ABD. Тогда ∠ABC =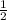 ∠ABD =
∠ABD = 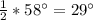 .
.
29°.
1) треугольник ABD равнобедренный, так как стороны AB=BC, следовательно и углы при основании равны, то есть А=Д
2) угол В равен 58°, сумма всех уголов в треугольнике равна ВСЕГДА 180, тогда (180-58):2= 61 - углы А и Д (объяснила в 1 действии почему)
3) В равнобедренном треугольнике высота, является биссектрисой и медианой, значит - ВС - биссиктриса - 58:2=29 угол АВС