Точка М равноудалена от сторон ромба, следовательно, проецируется в точку пересечения диагоналей ромба.
Расстояние от М до сторон равно длине отрезка МК, проведенного перпендикулярно к стороне ромба. Проекции этого отрезка равна радиусу вписанной в ромб окружности, который, проведенный в точку касания К со стороной ромба перпендикулярен ей.
Диаметр вписанной в ромб окружности равен высоте ромба.
а) Для стороны ромба:
Сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей. Ромб - параллелограмм, все стороны которого равны.
4 АВ²= 16²+12²=256+144=400
АВ²=100 ⇒ АВ=√100=10.
б) Для высоты ромба:
Площадь ромба равна половине произведения его диагоналей.
S=12•16:2=96 см²
Площадь ромба равна произведению высоты на его сторону:
S=h•a; 96=h•10; h=9,6 ⇒ r=9,6:2=4,8 см
Из прямоугольного ∆ МОК искомое расстояние
МО=√(MK²-OK²)=√(64-23,04)=6,4 см
* * *
Формула объема шарового сектора V=•πR²•h, где h - высота шарового сегмента с той же дугой в осевом сечении шара.
На рисунке приложения это КН.
∆ АОВ - прямоугольный, т.к. дуга АВ=90°
КО=АО•sin45° см
KH=R-OK=9-4,5√2=2,636 см²
V=•π•81•2,636=142,346π см³
* * *
Пусть вершина конуса М, его высота МО, радиус ОА=5 см, хорда АВ - основание сечения, его высота НМ=6 см является расстоянием от хорды до вершины конуса М.
Угол, под которым плоскость пересекает плоскость основания конуса - угол между двумя проведенными перпедикулярно к АВ лучами МН и ОН.
Тогда ∆ МОН - прямоугольный равнобедренный, НО=МО=МН•sin45°
Всего в урне 8 шаров, 3 из котрых белые, 5 черные. Следовательно шанс достать белый шар 3\8. поскольку шар после извлечения возвращается обратно в урну то соотношение шаров остаётся прежним и равно 3\8 для белых и 5\8 для чёрных. 1) вам нужна цепочка событий 3\8 3\8 5\8 для того чтобы соответствовать условию, итог не зависит от последовательности извлечения шаров и равен 3\8*3\8*5\8=45\512 или примерно 8,79% 2) в данном случае для простоты решения рассмотрим 2 случая, когда были извлечены ровно 2 белых шара и когда все 3 шара оказались белыми, а решение будет равно сумме вероятностей этих событий. расчёт для 2 белых шаров мы уже произвели в пункте 1, рассчитаем вероятность того что все 3 шара оказались белыми. 3\8*3\8*3\8=27\512 или около 5.27% чтобы найти наш итоговый шанс сложим наши решения 8.79+5.27=14,06%
Уважаемый, постом выше ваш ответ в любом случае неверен, так как шанс вытянуть не менее 2 белых включает шанс вытянуть 2 белых и шанс, что все 3 шара окажутся белыми, а значит шанс в задании 2 в любом случае будет выше.
Задание с перчатками: в ящике лежит 10 пар перчаток, то есть всего перчаток 20 штук 8 черных и 12 бежевых. поскольку в отличие от предыдущего задания предмет после извлечения не возвращают то шансы при 2 "вытаскивании" будут другими нежели исходные 8\20 для черных и 12\20 для бежевых. существует 2 решения задачи: 1. обе перчатки оказались черными 2. обе перчатки оказались бежевыми следовательно ответ будет равен сумме вероятностей этих событий. Для простоты вашего понимаю рассмотрим все варианты событий их будет 4:
1) первая перчатка чёрная 1.1) вторая перчатка чёрная 1.2) вторая перчатка бежевая
2) первая перчатка бежевая 2.1) вторая перчатка чёрная 2.2) вторая перчатка бежевая
нас устраивают только 2 из них когда цвета перчаток совпадают, вычислим вероятности, шанс вытянуть с 1 попытки черную перчатку равен 8\20, после этого общее количество перчаток станет равным 19, 7 из которых будут чёрные и ещё 12 бежевые. Шанс и вторую перчатку вытянуть тоже чёрную будет 7\19. вероятность того что эти события произойдут одно за другим равен 8\20*7\19=56\380 или около 14,7% шанс вытянуть 1 перчатку бежевую равен 12\20, после чего в ящике останется 19 перчаток из них 8 чёрных и 11 бежевых, шанс что и вторая тоже окажется бежевой равен 11\19, В итоге шанс вытянуть бежевую пару 12\20*11\19=132\380 или 34,7%
Точка М равноудалена от сторон ромба, следовательно, проецируется в точку пересечения диагоналей ромба.
Расстояние от М до сторон равно длине отрезка МК, проведенного перпендикулярно к стороне ромба. Проекции этого отрезка равна радиусу вписанной в ромб окружности, который, проведенный в точку касания К со стороной ромба перпендикулярен ей.
Диаметр вписанной в ромб окружности равен высоте ромба.
а) Для стороны ромба:
Сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей. Ромб - параллелограмм, все стороны которого равны.
4 АВ²= 16²+12²=256+144=400
АВ²=100 ⇒ АВ=√100=10.
б) Для высоты ромба:
Площадь ромба равна половине произведения его диагоналей.
S=12•16:2=96 см²
Площадь ромба равна произведению высоты на его сторону:
S=h•a; 96=h•10; h=9,6 ⇒ r=9,6:2=4,8 см
Из прямоугольного ∆ МОК искомое расстояние
МО=√(MK²-OK²)=√(64-23,04)=6,4 см
* * *
Формула объема шарового сектора V=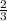
•πR²•h, где h - высота шарового сегмента с той же дугой в осевом сечении шара.
На рисунке приложения это КН.
∆ АОВ - прямоугольный, т.к. дуга АВ=90°
КО=АО•sin45°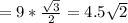
см
KH=R-OK=9-4,5√2=2,636 см²
V=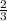
•π•81•2,636=142,346π см³
* * *
Пусть вершина конуса М, его высота МО, радиус ОА=5 см, хорда АВ - основание сечения, его высота НМ=6 см является расстоянием от хорды до вершины конуса М.
Угол, под которым плоскость пересекает плоскость основания конуса - угол между двумя проведенными перпедикулярно к АВ лучами МН и ОН.
Тогда ∆ МОН - прямоугольный равнобедренный, НО=МО=МН•sin45°
V=S•h=πr²•h
V=π•25•3√2):3=π•25√2 см³
1) вам нужна цепочка событий 3\8 3\8 5\8 для того чтобы соответствовать условию, итог не зависит от последовательности извлечения шаров и равен 3\8*3\8*5\8=45\512 или примерно 8,79%
2) в данном случае для простоты решения рассмотрим 2 случая, когда были извлечены ровно 2 белых шара и когда все 3 шара оказались белыми, а решение будет равно сумме вероятностей этих событий. расчёт для 2 белых шаров мы уже произвели в пункте 1, рассчитаем вероятность того что все 3 шара оказались белыми. 3\8*3\8*3\8=27\512 или около 5.27% чтобы найти наш итоговый шанс сложим наши решения 8.79+5.27=14,06%
Уважаемый, постом выше ваш ответ в любом случае неверен, так как шанс вытянуть не менее 2 белых включает шанс вытянуть 2 белых и шанс, что все 3 шара окажутся белыми, а значит шанс в задании 2 в любом случае будет выше.
Задание с перчатками: в ящике лежит 10 пар перчаток, то есть всего перчаток 20 штук 8 черных и 12 бежевых. поскольку в отличие от предыдущего задания предмет после извлечения не возвращают то шансы при 2 "вытаскивании" будут другими нежели исходные 8\20 для черных и 12\20 для бежевых. существует 2 решения задачи:
1. обе перчатки оказались черными
2. обе перчатки оказались бежевыми
следовательно ответ будет равен сумме вероятностей этих событий.
Для простоты вашего понимаю рассмотрим все варианты событий их будет 4:
1) первая перчатка чёрная
1.1) вторая перчатка чёрная
1.2) вторая перчатка бежевая
2) первая перчатка бежевая
2.1) вторая перчатка чёрная
2.2) вторая перчатка бежевая
нас устраивают только 2 из них когда цвета перчаток совпадают, вычислим вероятности, шанс вытянуть с 1 попытки черную перчатку равен 8\20, после этого общее количество перчаток станет равным 19, 7 из которых будут чёрные и ещё 12 бежевые. Шанс и вторую перчатку вытянуть тоже чёрную будет 7\19. вероятность того что эти события произойдут одно за другим равен 8\20*7\19=56\380 или около 14,7%
шанс вытянуть 1 перчатку бежевую равен 12\20, после чего в ящике останется 19 перчаток из них 8 чёрных и 11 бежевых, шанс что и вторая тоже окажется бежевой равен 11\19, В итоге шанс вытянуть бежевую пару 12\20*11\19=132\380 или 34,7%
Итоговый шанс вытянуть пару равен 14,7*34,7=49,4%