у нас ABCD прямоугольник, мы с легкостью найдём его диагональ CA.
рассмотрим треугольник допустим ABC, мы знаем что у него угол B = 90 градусам так как он часть большого прямоугольника, и знаем две его стороны, допустим BC = 3см, а ВА = 6см. По теореме Пифагора найдём гипотенузу СА. СА=см.
теперь рассмотрим треугольник С1СА, он тоже прямоугольный, угол С=90 градусов. Нам известно сколько равно СА, и сколько равна диагональ С1А. По теореме Пифагора найдём высоту СС1. СС1= см. Теперь мы знаем высоту СС1=Н.
Найдём Sбоковую. Sбок= Р(основы)*Н. Р = 3+3+6+6=18см => Sбок = 18*3= 54см^2. Теперь найдём Sосновы. Так как основание прямоугольник, то площадь будет равна произведению сторон Sосновы = 3*6= 18см^2.
и теперь наконец-то вернёмся к полной площади Sполная = 54+2*18= 90см^2.
Параллельность двух прямых можно доказать на основе теоремы, согласно которой, два проведенных перпендикуляра по отношению к одной прямой, будут параллельны. Существуют определенные признаки параллельности прямых – всего их три, и все их мы рассмотрим более конкретно. Первый признак параллельности Прямые параллельны, если при пересечении их третьей прямой, образуемые внутренние углы, лежащие накрест, будут равны. Допустим, при пересечении прямых АВ и СD прямой линией ЕF, были образованы углы /1 и /2. Они равны, так как прямая линия ЕF проходит под одним уклоном по отношению к двум остальным прямым. В местах пересечения линий, ставим точки Ки L – у нас получился отрезок секущей ЕF. Находим его середину и ставим точку О (черт. 189). На прямую АВ опускаем перпендикуляр из точки О. Назовем его ОМ. Продолжаем перпендикуляр до тех пор, пока он не пересечется с прямой СD. В результате, первоначальная прямая АВ строго перпендикулярна МN, а это значит, что и СD_|_МN, но это утверждение требует доказательства. В результате проведения перпендикуляра и линии пересечения, у нас образовалось два треугольника. Один из них – МОЕ, второй – NОК. Рассмотрим их более подробно. признаки параллельности прямых 7 класс Данные треугольники равны, поскольку, в соответствии с условиями теоремы, /1 =/2, а в соответствии с построением треугольников, сторона ОK = стороне ОL. Угол МОL =/NОК, поскольку это вертикальные углы. Из этого следует, что сторона и два угла, прилежащие к ней одного из треугольников соответственно равны стороне и двум углам, прилежащим к ней, другого из треугольников. Таким образом, треугольник МОL =треугольникуNОК, а значит, и угол LМО = углу КNО, но нам известно, что/LМО прямой, значит, и соответствующий ему, угол КNО тоже прямой. То есть, нам удалось доказать, что к прямой МN, как прямая АВ, так и прямая СD перпендикулярны. То есть, АВ и СD по отношению друг к другу являются параллельными. Это нам и требовалось доказать. Рассмотрим остальные признаки параллельности прямых (7 класс), которые отличаются от первого признака по доказательства. Второй признак параллельности Согласно второму признаку параллельности прямых, нам необходимо доказать, что углы, полученные в процессе пересечения параллельных прямых АВ и СD прямой ЕF, будут равны. Таким образом, признаки параллельности двух прямых, как первый, так и второй, основывается на равности углов, получаемых при пересечении их третьей линией. Допускаем, что /3 = /2, а угол 1 = /3, поскольку он вертикален ему. Таким образом, и /2 будет равен углу1, однако следует учитывать, что как угол 1, так и угол 2 являются внутренними, накрест лежащими углами. Следовательно, нам остается применить свои знания, а именно то, что два отрезка будут параллельными, если при их пересечении третьей прямой образованные, накрест лежащие углы будут равными. Таким образом, мы выяснили, что АВ || СD. Нам удалось доказать, что при условии параллельности двух перпендикуляров к одной прямой, согласно соответствующей теореме, признак параллельности прямых очевиден. Третий признак параллельности Существует еще и третий признак параллельности, который доказывается посредством суммы односторонних внутренних углов. Такое доказательство признака параллельности прямых позволяет сделать вывод, что две прямые будут параллельны, если при пересечении их третье прямой, сумма полученных односторонних внутренних углов, будет равна 2d.
ку) кр на 176 стр задание 5? :)
го хэлпану :
как мы знаем Sполная = Sбоковая + 2Sосновы.
у нас ABCD прямоугольник, мы с легкостью найдём его диагональ CA.
рассмотрим треугольник допустим ABC, мы знаем что у него угол B = 90 градусам так как он часть большого прямоугольника, и знаем две его стороны, допустим BC = 3см, а ВА = 6см. По теореме Пифагора найдём гипотенузу СА. СА=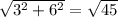
см.
теперь рассмотрим треугольник С1СА, он тоже прямоугольный, угол С=90 градусов. Нам известно сколько равно СА, и сколько равна диагональ С1А. По теореме Пифагора найдём высоту СС1. СС1=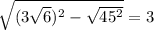
см. Теперь мы знаем высоту СС1=Н.
Найдём Sбоковую. Sбок= Р(основы)*Н. Р = 3+3+6+6=18см => Sбок = 18*3= 54см^2. Теперь найдём Sосновы. Так как основание прямоугольник, то площадь будет равна произведению сторон Sосновы = 3*6= 18см^2.
и теперь наконец-то вернёмся к полной площади Sполная = 54+2*18= 90см^2.
С тебя лайк :)