Определите косинус угла между треугольником A B1C и плоскостью основания куба ABCDA1B1C1D1 со стороной 1.
Объяснение:
Нужно найти двугранный угол В₁АСВ.
В кубе все грани квадраты. Диагональ квадрата равна √(1²+1²)=√2 , половина диагонали 0,5√2. Пусть О-точка пересечения диагоналей основания.
Диагонали квадрата взаимно перпендикулярны , значит ОВ⊥АС. Тк. проекция ОВ⊥АС ,прямой лежащей в плоскости , то и наклонная В₁О⊥АС. Поэтому ∠В₁ОВ-линейный угол двугранного В₁АСВ.
ΔВВ₁О- прямоугольный , tg∠В₁ОВ= , tg∠В₁ОВ= =√2.
1+tg²∠В₁ОВ= , 1+√2²= ,cos∠B₁OB= , cos∠B₁OB=
Определите косинус угла между треугольником A B1C и плоскостью основания куба ABCDA1B1C1D1 со стороной 1.
Объяснение:
Нужно найти двугранный угол В₁АСВ.
В кубе все грани квадраты. Диагональ квадрата равна √(1²+1²)=√2 , половина диагонали 0,5√2. Пусть О-точка пересечения диагоналей основания.
Диагонали квадрата взаимно перпендикулярны , значит ОВ⊥АС. Тк. проекция ОВ⊥АС ,прямой лежащей в плоскости , то и наклонная В₁О⊥АС. Поэтому ∠В₁ОВ-линейный угол двугранного В₁АСВ.
ΔВВ₁О- прямоугольный , tg∠В₁ОВ=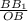
, tg∠В₁ОВ= 
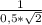=√2.
1+tg²∠В₁ОВ=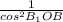
, 1+√2²=
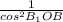,cos∠B₁OB=
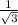, cos∠B₁OB=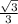
р=(15+14+13)/2=21
S(Δ АВС)=√21·(21-15)·(21-14)·(21-13)=84 см
S(ΔABA₁)=S(ΔACA₁)
В этих треугольниках основания A₁В=СA₁, а высота общая.
S(ΔACA₁)=42 см
Биссектриса ВВ₁ делит сторону АС в отношении 15:14
пропорционально прилежащим сторонам треугольника
АВ₁ =15 АС/29
Биссектриса ВР делит сторону АА₁ треугольника АВА₁ в отношении 15:7
AP=15AA₁ /22
S(ΔAPB₁ )=AP·AB₁ ·sin ∠A₁ AC/2=
=(15 ·AA₁ /22)·(15AC/29)·sin ∠A₁ AC/2=
=(225/638)·(AA·AC·sin ∠A₁ AC/2)=(225/638)·42
S(четырехугольника PA₁CB₁)=S(ΔAA₁C)-A(ΔAPB₁)=42-(225/638)·42=
=42·(1-(225/638))=413·42/638≈27,2