Нужна ЗНАТОКОВ ПО ГЕОМЕТРИИ. Только, кто понимает.
Даны точки М1 (1,2, -1) и М2 (3,4, -2)
найти:
1) координаты, длину, направляющие косинусы и орт вектора М1М2.
2) скалярное произведение (М1М2 * М1М3) М3 = (- 4,1, -2)

Показать ответ

Ответ:

sofiakuznetsova2004

24.02.2023 11:41

Объяснение:

Итак, что вообще значит решить треугольник?

Решить треугольник - это значит, найти все элементы треугольника(то есть, его три стороны и три угла)

Но у нас задача упрощена: нам надо найти два угла и одну сторону.

Чтобы найти сторону треугольника, мы запишем теорему косинусов:

c^2 = a^2 + b^2 - 2ab*cosB

Где c - это сторона, которую мы ищем; a и b - две другие стороны треугольника. cosB - это косинус угла, лежащий напротив той стороны, которую мы ищем.

Подставим данные в формулу(кстати cos60 =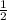 $\frac{1}{2}$ )

c^2 = 25 + 21^2 - 2 * 5 * 21 * 0,5

Вычислив всю эту гадость, получаем:

c^2 = 361

И когда ученики находят значение с^2, они начинают прыгать от счастья и вносят в ответ число 361, что конечно же неверно, так как 361 - это КВАДРАТ той стороны, которую мы ищем. А чтобы найти саму сторону, нам надо извлечь квадратный корень из 361.

c =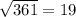 $\sqrt{361} = 19$

Ну и нам остается найти два угла треугольника.

Как это сделать?

Для каждого треугольника справедлива такая херня, которая называется теоремой синусов.

$\frac{a}{sinA} = \frac{ b}{sinB} = \frac{c}{sinC}$

Если говорить словами, а не арабскими иероглифами, то получается такая формулировка: стороны треугольника пропорциональны синусам углов, напротив которых эти стороны лежат.

Давай запишем теорему синусов для нашего треугольника:

$\frac{AC}{sin60} = \frac{21}{sinA}$

Не забывай, что sin60 =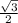 $\frac{\sqrt{3} }{2}$

Исходя из свойств пропорции, мы можем выразить sinA =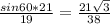 $\frac{sin60 * 21}{19} = \frac{21\sqrt{3} }{38}$

Не бойся того, что мы получили в ответе такое страшное число: в этом нет ничего сверхъестественного.

Теперь, посмотрев в Интернете или посчитав на калькуляторе, мы получаем, что угол А равен 73 градусам.

Другой угол ищем проще:

Сумма углов в треугольнике равна 180 градусов.

Тогда угол С будет равен 180 - 73 - 60 = 47 градусов

Все. Задача решена.

0,0(0 оценок)

Ответ:

Убийца967

18.04.2023 09:06

а) Доказательство:

АВ = ВМ, по условию, значит треугольник АВМ - равнобедренный. По свойству равнобедренного треугольника угол ВАМ = углу ВМА.

По свойству параллелограмма ВС параллельно АD, АС - секущая, значит угол АМВ = углу МАD, из вышесказанного следует, что угол ВАМ = углу МАD, значит АМ - биссектрисса

б) Решение:

АВ = СD по свойству параллелограмма,а АВ = ВМ из доказательства. Значит АВ = ВМ = СD = 8 см

МС = 4 по условию. ВС = ВМ + МС = 8 + 4 = 12. По свойству параллелограмма ВС = АD = 12

теперь можем найти площадь: Р = АВ + ВС + СD + DА = 8 + 12 + 8 + 12 = 40 см