Обчисліть об'єм CO2 ща нормальних умов масою 44г

это химия извиняюсь

Вертикальные углы равны.

Сумма смежных углов равна 180 градусов.

Если 1 угол равен 30 градусам, то вертикальный с ним угол равен тоже 30 градусам,  смежный равен 150 градусам. Вертикальный смежному 150 градусов.

Дано:

пересекающиеся прямые.

угол 1=30 градусов

Найти: углы 2;3;4.

Решение: угол 3 = угол 1 = 30 градусов(вертикальные углы)

угол 2 = угол 4 = 180 градуов минус угол 1(смежные углы) = 180 градусов минус 30 градусов = 150 градусов

ответ: Угол 2= 150 гр.

           Угол 3= 30 гр.

           Угол 4 = 150 гр.

∠ 1 = ?°, на 55° больше, чем ∠ 2.

∠ 2 = ?°

Оба угла являются смежными.

Пусть x° равен смежный ∠ 2, тогда ∠ 1 равен (55+x)˚. Зная, что свойство смежных углов всегда содержит сумму 180°, составим уравнение с переменными и решим задачу алгебраическим

Составление математической модели:

Работа с математической моделью:

Поскольку уравнение имеет переменные, раскроем скобки и найдём значение переменных:

Теперь, зная что число с переменной и число без переменной в данном случае вычислить невозможно, перенесем число без переменной в правую часть уравнения (число становится отрицательным):

Затем вычислим полученный пример, находящийся в правой части уравнения:

Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель:

ответ математической модели:

Исходя из значения данного примера, получим корень уравнения:

˚ - ∠ 2.

Теперь остаётся только узнать величину ∠ 1:

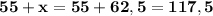˚ - ∠ 1.