Обозначим вершину конуса через S, хорду через AB, основание высоты конуса через H, середину хорды через К
Рассмотрим прямоугольный треугольник SHK, образованный высотой конуса и серединой хорды. Катет SH, являющийся высотой конуса равен 10 см, противолежащий угол SKH равен 30градусам. Значит гипотенуза KS этого треугольника равна 20см, а второй катет KH = 10
Рассмотрим треугольник ABH, образованный хордой и двумя радиусами. Радиусы AH = BH равны между собой и угол AHB между ними равен 60 - значит треугольник равносторонний.
Его высоту HK (опущенную на хорду) только что вычислили как 10.
Отсюда находим, что длина стороны равностороннего треугольника ABH равна 20.
Сечение является равнобедренным треугольником SAB с высотой SK = гипотенузе первого треуольника и AB основанием = хорде. Его площадь = 20 * 20 / 2 = 200
1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM=а . Найдите площадь поверхности пирамиды. --- Площадь поверхности пирамиды состоит из площади основания и 2-х пар равных граней - прямоугольных треугольников (⊿ MDA=⊿ MDC;⊿ MAB=⊿ MCB): АМ и МС перпендикулярны сторонам квадрата ( по т. о 3-х перпендикулярах), а МD перпендикулярна его плоскости по условию. S полн= S АВСD+ 2S (MAВ)+2S (MCD) 2S (MAD)=(a²:2)•2=a² 2S (MАВ)=АВ•MA MA=a√2 (треугольник МАD равнобедренный прямоугольный) 2S (MАВ)=2•(а•а√2):2=а²√2 S(ABCD)=a² S полн=a²+а²+a²√2=a²(2+√2) ————————————————————————— 2. Основание прямого параллелепипеда АВСDA’B’C’D' - параллелограмм АВСД, стороны которого равны а√2 и 2а , острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: а) меньшую высоту параллелограмма; б)угол между плоскостью АВС1 и плоскостью основания; в)Площадь боковой поверхности параллелепипеда; г)Площадь поверхности параллелепипеда.
а)
меньшая высота CН параллелограмма ABCD идет из вершины C к большей его стороне АВ.
∆ ВСН - прямоугольный, угол СВН=45° по условию.=>
СН=ВС•sin45°=a√2•√2/2=a
б)
Параллелепипед прямой,⇒ ребро СС’ перпендикулярно плоскости основания и сторонам и является высотой параллелепипеда.
СС’=CH=a
СН перпендикулярна АВ, С'Н⊥АВ по т. о 3-х перпендикулярах
а так как СС’=СH (по условию), треугольник НСС’ равнобедренный прямоугольный.
Угол СНС’ между плоскостью АВС1 и плоскостью основания из равнобедренного прямоугольного треугольника СНС’=45°
в)
Площадь боковой поверхности параллелепипеда равна произведению его периметра на высоту:
S бок=2•( 2а+а√2)•а=4а²+2а²√2=2а²(2+√2)
г)
Площадь поверхности параллелепипеда - сумма площадей 2-х оснований и боковой поверхности.
Обозначим вершину конуса через S, хорду через AB, основание высоты конуса через H, середину хорды через К
Рассмотрим прямоугольный треугольник SHK, образованный высотой конуса и серединой хорды. Катет SH, являющийся высотой конуса равен 10 см, противолежащий угол SKH равен 30градусам. Значит гипотенуза KS этого треугольника равна 20см, а второй катет KH = 10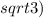
Рассмотрим треугольник ABH, образованный хордой и двумя радиусами. Радиусы AH = BH равны между собой и угол AHB между ними равен 60 - значит треугольник равносторонний.
Его высоту HK (опущенную на хорду) только что вычислили как 10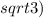 .
.
Отсюда находим, что длина стороны равностороннего треугольника ABH равна 20.
Сечение является равнобедренным треугольником SAB с высотой SK = гипотенузе первого треуольника и AB основанием = хорде. Его площадь = 20 * 20 / 2 = 200
---
Площадь поверхности пирамиды состоит из площади основания и 2-х пар равных граней - прямоугольных треугольников (⊿ MDA=⊿ MDC;⊿ MAB=⊿ MCB): АМ и МС перпендикулярны сторонам квадрата ( по т. о 3-х перпендикулярах), а МD перпендикулярна его плоскости по условию.
S полн= S АВСD+ 2S (MAВ)+2S (MCD)
2S (MAD)=(a²:2)•2=a²
2S (MАВ)=АВ•MA
MA=a√2 (треугольник МАD равнобедренный прямоугольный)
2S (MАВ)=2•(а•а√2):2=а²√2
S(ABCD)=a²
S полн=a²+а²+a²√2=a²(2+√2)
—————————————————————————
2.
Основание прямого параллелепипеда АВСDA’B’C’D' - параллелограмм АВСД, стороны которого равны а√2 и 2а , острый угол равен 45°.
Высота параллелепипеда равна меньшей высоте параллелограмма.
Найдите:
а) меньшую высоту параллелограмма;
б)угол между плоскостью АВС1 и плоскостью основания;
в)Площадь боковой поверхности параллелепипеда;
г)Площадь поверхности параллелепипеда.
а)
меньшая высота CН параллелограмма ABCD идет из вершины C к большей его стороне АВ.
∆ ВСН - прямоугольный, угол СВН=45° по условию.=>
СН=ВС•sin45°=a√2•√2/2=a
б)
Параллелепипед прямой,⇒ ребро СС’ перпендикулярно плоскости основания и сторонам и является высотой параллелепипеда.
СС’=CH=a
СН перпендикулярна АВ, С'Н⊥АВ по т. о 3-х перпендикулярах
а так как СС’=СH (по условию), треугольник НСС’ равнобедренный прямоугольный.
Угол СНС’ между плоскостью АВС1 и плоскостью основания из равнобедренного прямоугольного треугольника СНС’=45°
в)
Площадь боковой поверхности параллелепипеда равна произведению его периметра на высоту:
S бок=2•( 2а+а√2)•а=4а²+2а²√2=2а²(2+√2)
г)
Площадь поверхности параллелепипеда - сумма площадей 2-х оснований и боковой поверхности.
S (ABCD)=СH•AВ=a•2a=2a²
Оснований два.
S полн=2•2a²+2а²(2+√2)=2а²(4+√2)