1.1. Строим равнобедренный прямоугольный треугольник с катетами =a
обозначим гипотенузу с
По теореме Пифагора c²=a²+a²=2a²
1.2 Строим равнобедренный прямоугольный треугольник с катетами =с
обозначим гипотенузу с₁
По теореме Пифагора c₁²=с²+с²=2a²+2a²=4a²
2) аналогично пункту 1) строим отрезок квадрат которого =4b²
2.1. Строим равнобедренный прямоугольный треугольник с катетами =b
обозначим гипотенузу с₂
По теореме Пифагора c₂²=b²+b²=b²
2.2 Строим равнобедренный прямоугольный треугольник с катетами =с
обозначим гипотенузу с₃
По теореме Пифагора c₃²=с₂²+с₂²=2b²+2b²=4b²
3) построение отрезка квадрат которого = 5ab
Строим окружность диаметром a+5b
на диаметре откладываем отрезки a и 5b
обозначим точку которая делит диаметр на отрезки а и 5b D
через точку D проводим перпендикуляр до пересечения с оркужностью в точке С получаем прямоугольный треугольник в котором отрезок CD - высота обозначим ее как h
так как высота является средникм геометрическим проекций катетов то h=√(5ab) и h²=5ab
4) строим прямоугольный треугольник с катетами с₁ и с₃
обозначим его гипотенузу с₄
по теореме Пифагора с₄²=с₁²+с₃²=4a²+4b²
5) строим прямоугольный треугольник с катетами с₄ и h
обозначим его гипотенузу с₅
по теореме Пифагора с₅²=с₄²+h²=4a²+4b²+5ab=4a²+5ab+4b²
Продолжим касательные до их пересечения в т.Р.
ОА⊥АС и О1С⊥АС ( радиусы, проведенные в точку касания.
Из т.О проведем параллельно АС прямую до пересечения с СО1 в т.Н.
Четырехугольник АОНС - прямоугольник. СН=АО=r=12 ⇒
О1Н=20-12=8
⊿ ОНО1 - прямоугольный. ОО1=12+20=32.
По т.Пифагора
ОН=√(OO1²-O1H²)=√(32²-8²)=√960=8√15
cos∠HOO1=OH:OO1=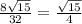
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.⇒
РС=РD, PA=PB ⇒ BD=AC=8√15
∆ СРD равнобедренный, ∆ РАВ равнобедренный ⇒
биссектриса АО1 перпендикулярна АВ и СD
∠СРО1=∠DPO1
Расстояние между АВ и СD - длина общего между ними перпендикуляра.
Проведем ВМ || РО1
ВМ⊥АВ и ВМ⊥СD.
∆ ВМD прямоугольный. ∠МВD=∠O1PD
ВМ=BD•cosO1PD=8√15•√15:4=30
Объяснение:
1) построение отрезка квадрат которого =4a²
1.1. Строим равнобедренный прямоугольный треугольник с катетами =a
обозначим гипотенузу с
По теореме Пифагора c²=a²+a²=2a²
1.2 Строим равнобедренный прямоугольный треугольник с катетами =с
обозначим гипотенузу с₁
По теореме Пифагора c₁²=с²+с²=2a²+2a²=4a²
2) аналогично пункту 1) строим отрезок квадрат которого =4b²
2.1. Строим равнобедренный прямоугольный треугольник с катетами =b
обозначим гипотенузу с₂
По теореме Пифагора c₂²=b²+b²=b²
2.2 Строим равнобедренный прямоугольный треугольник с катетами =с
обозначим гипотенузу с₃
По теореме Пифагора c₃²=с₂²+с₂²=2b²+2b²=4b²
3) построение отрезка квадрат которого = 5ab
Строим окружность диаметром a+5b
на диаметре откладываем отрезки a и 5b
обозначим точку которая делит диаметр на отрезки а и 5b D
через точку D проводим перпендикуляр до пересечения с оркужностью в точке С получаем прямоугольный треугольник в котором отрезок CD - высота обозначим ее как h
так как высота является средникм геометрическим проекций катетов то h=√(5ab) и h²=5ab
4) строим прямоугольный треугольник с катетами с₁ и с₃
обозначим его гипотенузу с₄
по теореме Пифагора с₄²=с₁²+с₃²=4a²+4b²
5) строим прямоугольный треугольник с катетами с₄ и h
обозначим его гипотенузу с₅
по теореме Пифагора с₅²=с₄²+h²=4a²+4b²+5ab=4a²+5ab+4b²
c₅= √(4a²+5ab+4b²)