Диагонали ромба взаимно перпендикулярны. AOD - прямоугольный треугольник. ОР - высота из прямого угла в треугольнике AOD. ОР=√(АР*РD)=√(6√3*2√3)=6см. По Пифагору АО=√(АР²+ОР²)=√(108+36)=12см. R=AJ=JO=JP = АО/2 = 6см. Площадь круга Sк=π*R²=36π. В прямоугольном треугольнике АРО катет ОР равен половине гипотенузы АО, значит <PAO=30°, <РАК=60° (так как АО - биссектриса <PAK) => дуга РОК=120°. <PJK=120°(центральный угол, опирающийся на дугу РОК). РН=0,5*АР=3√3см (катет против угла 30°). AH=√(АР²-РH²)=√(108-27)=9см. Площадь треугольника АКР равна Sapk=AH*PH=9*3√3=27√3см². Площадь сегмента КОР равна Skop=(R²/2)*(π*α/180 -Sinα) - формула. В нашем случае α=<PKJ =120°. Skop=(36/2)*(π*120/180 -√3/2) Skop=(12π-9√3)см². Искомая площадь равна S=Sк-Sapk-Skop = 36π-27√3-12π+9√3 = (24π-18√3)см².
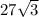 ед².
ед².
Объяснение:Обозначим данную пирамиду буквами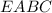 .
.
Проведём высоту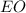 . Точка
. Точка 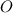 - центр
- центр 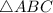 - точка пересечения, медиан, высот и биссектрис треугольника.
- точка пересечения, медиан, высот и биссектрис треугольника.
Проведём апофему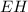 (апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне
(апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне 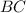 основания пирамиды.
основания пирамиды.
Т.к. данная пирамида - правильная, треугольная ⇒ основание пирамиды - правильный треугольник.
Проведём высоту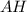 в
в 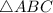 .
.
Т.к.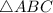 - равносторонний ⇒
- равносторонний ⇒ 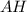 - высота, медиана, биссектриса.
- высота, медиана, биссектриса.
Высота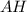 и апофема
и апофема 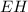 имеют общее основание, а именно точку
имеют общее основание, а именно точку 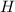 , т.к.
, т.к. 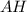 - медиана, а апофема
- медиана, а апофема 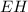 делит
делит 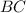 пополам (по свойству).
пополам (по свойству).
Рассмотрим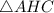 :
:
Найдём высоту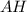 по теореме Пифагора:
по теореме Пифагора: 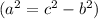
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Точка O - пересечение медиан и делит их в отношении 2 : 1, считая от вершины.
Рассмотрим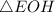 :
:
Если угол прямоугольного треугольника равен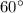 , то напротив лежащий катет равен произведению меньшего катета на
, то напротив лежащий катет равен произведению меньшего катета на 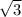 .
.
Найдём апофему по теореме Пифагора: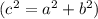
====================================================
⇒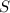 бок. поверх. =
бок. поверх. = 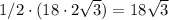 ед².
ед².
⇒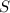 полн. поверх. =
полн. поверх. = 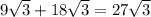 ед².
ед².
AOD - прямоугольный треугольник.
ОР - высота из прямого угла в треугольнике AOD.
ОР=√(АР*РD)=√(6√3*2√3)=6см.
По Пифагору АО=√(АР²+ОР²)=√(108+36)=12см.
R=AJ=JO=JP = АО/2 = 6см.
Площадь круга Sк=π*R²=36π.
В прямоугольном треугольнике АРО катет ОР равен половине
гипотенузы АО, значит <PAO=30°,
<РАК=60° (так как АО - биссектриса <PAK) => дуга РОК=120°.
<PJK=120°(центральный угол, опирающийся на дугу РОК).
РН=0,5*АР=3√3см (катет против угла 30°).
AH=√(АР²-РH²)=√(108-27)=9см.
Площадь треугольника АКР равна
Sapk=AH*PH=9*3√3=27√3см².
Площадь сегмента КОР равна
Skop=(R²/2)*(π*α/180 -Sinα) - формула.
В нашем случае α=<PKJ =120°.
Skop=(36/2)*(π*120/180 -√3/2)
Skop=(12π-9√3)см².
Искомая площадь равна
S=Sк-Sapk-Skop = 36π-27√3-12π+9√3 = (24π-18√3)см².