1. как изменяется площадь прямоугольника, если одну его сторону уменьшить в три раза, а другую уменьшить в два раза. Выбири правильный ответ 1. Уменьшится а шесть раз 2.Увеличится в шесть раз 3. уменьшится в три раза 4. не изменится. ОТВЕТ: 1
2. Для облицовки прямоугольной стены, длины которой 6 м, в высота 2 м, потребаволось 300 квадратных плиток. Найдите размер 1 плитки. 6*2:300=0,04 м кв
3.тупой угол ромба равен 150градусов, а его сторона равна 6 см. УСЛОВИЕ ПРОВЕРЬ
4.В трапеции ABCD основание ВС равно 5 см, а основание AD равно 35смквадратных . УСЛОВИЕ ПРОВЕРЬ
5.Сторона прямоугольника равна 15 см, а его диагональ равна 17см. Найдите плошадь прямоугольника. 120 см кв
7.В окружности с радиусом 65см проведёных две паралельны хорды А1В1 и А2В2 соответственно равны 126 см и 112 см, Найдите растояние между хордами. подумать надо
Площадь равнобедренной трапеции ABCD равна 48 см². Высота трапеции равна 4√3 см ,боковая сторона 5√3 см .Боковые стороны AB и CD продолжили до пересечения в точке О .Найдите площадь треугольника AOD в ( у см² ).
Объяснение:
1) Пусть МВ⊥АД, СР⊥АД. Тогда ΔАВМ=ΔДСР как прямоугольные по гипотенузе (АВ=СД) и острому углу (∠А=∠Д , как углы при основании равнобедренной трапеции)⇒ АМ=РД .
2)ΔАВМ-прямоугольный , по т. Пифагора АМ=√(25*3-16*3)=3√3 (см), значит РД=3√3 см.
ОТВЕТ: 1
2. Для облицовки прямоугольной стены, длины которой 6 м, в высота 2 м, потребаволось 300 квадратных плиток. Найдите размер 1 плитки.
6*2:300=0,04 м кв
3.тупой угол ромба равен 150градусов, а его сторона равна 6 см.
УСЛОВИЕ ПРОВЕРЬ
4.В трапеции ABCD основание ВС равно 5 см, а основание AD равно 35смквадратных .
УСЛОВИЕ ПРОВЕРЬ
5.Сторона прямоугольника равна 15 см, а его диагональ равна 17см. Найдите плошадь прямоугольника.
120 см кв
7.В окружности с радиусом 65см проведёных две паралельны хорды А1В1 и А2В2 соответственно равны 126 см и 112 см, Найдите растояние между хордами.
подумать надо
Площадь равнобедренной трапеции ABCD равна 48 см². Высота трапеции равна 4√3 см ,боковая сторона 5√3 см .Боковые стороны AB и CD продолжили до пересечения в точке О .Найдите площадь треугольника AOD в ( у см² ).
Объяснение:
1) Пусть МВ⊥АД, СР⊥АД. Тогда ΔАВМ=ΔДСР как прямоугольные по гипотенузе (АВ=СД) и острому углу (∠А=∠Д , как углы при основании равнобедренной трапеции)⇒ АМ=РД .
2)ΔАВМ-прямоугольный , по т. Пифагора АМ=√(25*3-16*3)=3√3 (см), значит РД=3√3 см.
3)Длина АД=АМ+МР+РД=6√3+МР . Пусть МН=у, АД=6√3+2у ⇒ВС=6√3+2у .
S(трап)=1/2*(АД+ВС)*ЕН , 48=1/2*(6√3+4у)*4√3 ,6√3+4у=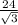 ,
,
4у= 8√3-6√3 , у=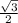 ⇒ ВЕ=
⇒ ВЕ=
4) АН=3√3-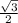 =3,5√3 (см).
=3,5√3 (см).
ΔОВЕ подобен ΔОАН по двум углам: ∠О-общий,∠ВЕО=∠АНО=90°, значит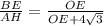 ,
, 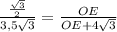 ,
, 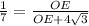 ,
,
OE=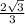 см
см
5) Высота ОН=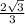 +4√3 =
+4√3 = 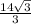 (см) , АД=6√3+√3=7√3 (см).
(см) , АД=6√3+√3=7√3 (см).
S(AOД)=1/2*АД*ОН , S(AOД=1/2* 7√3*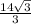 = 49(см²).
= 49(см²).