прямая ad так же принадлежит этой плоскости, но кроме того, она принадлежит и плоскости abd, а значит, найдя точку пересечения этих прямых (а они будут пересекаться так как лежат в одной плоскости и не параллельны) мы и найдем точку пересечения fd1 с плоскостью abd. на рисунке это точка z (прошу прощения у меня довольно криво)
2. так как плоскости a1b1c1 и abc параллельны, то и линии пересечения этих плоскостей третьей параллельны (свойство параллельных плоскостей)
так как мы уже нашли точку пересечения плоскости fb1d1 с плоскостью abd (предыдущее ), то проводим параллельную прямую через нее . чертёж не смогла вставить . поищи в инете .
дано:
прямая fd1 принадлежит плоскости aa1d
решение
прямая ad так же принадлежит этой плоскости, но кроме того, она принадлежит и плоскости abd, а значит, найдя точку пересечения этих прямых (а они будут пересекаться так как лежат в одной плоскости и не параллельны) мы и найдем точку пересечения fd1 с плоскостью abd. на рисунке это точка z (прошу прощения у меня довольно криво)
2. так как плоскости a1b1c1 и abc параллельны, то и линии пересечения этих плоскостей третьей параллельны (свойство параллельных плоскостей)
так как мы уже нашли точку пересечения плоскости fb1d1 с плоскостью abd (предыдущее ), то проводим параллельную прямую через нее . чертёж не смогла вставить . поищи в инете .
Відповідь:
Пояснення:
Дано: коло O; коло O1; OB = 5; O1B1 = 3; B∈AB; B1∈AB; AB1 = 4
Знайти: OO1
Розв'язання:
Розглянемо ΔAOB і ΔAO1B1.
∠A - спільний; OB⊥AB, O1B1⊥AB (за властивістю дотичної та радіуса, проведеного в точку дотику). Отже ΔAOB подібний ΔAO1B1 (за двома кутами).
В ΔAO1B1 за теоремою Піфагора знайдемо гіпотенузу AO1
AO1^2 = AB1^2 + O1B1^2
AO1^2 = 4^2 + 3^2 = 16 + 9 = 25
AO1 =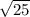 = 5
= 5
У подібних трикутниках відповідні сторони пропорційні:
OB/O1B1 = AO/AO1
5/3 = AO/5
AO = 5*5/3
AO = 25/3
OO1 = AO - AO1
OO1 = 25/3 - 5 = 10/3
OO1 ≈ 3,3