В треугольнике ABC PK-средняя линия треугольника,параллельная AB, P (2;3), K (-1;2) и С(0;0). Напишите уравнение прямой,содержащей сторону AB.
Объяснение:
Уравнение прямой у=кх+b . Ищем числа а,b.
1) РК-средняя линия ⇒ РК║АВ. У параллельных прямых одинаковое к. Ищем к прямой РК.
P (2;3), {3=2k+b
K (-1;2), {2=-1k+b. Вычтем из первого уравнения второе , получим 1=3k,k=1/3. Такое же k будет у прямой АВ.
2)Найдем координаты точки А, используя формулу середины отрезка, тк РК-средняя линия.
,A(4;6).
3)Составляем уравнение прямой у=кх+b ,содержащей сторону AB используя k=1/3 ,A(4;6).
6=1/3*4+b => b= . Тогда .
orjabinina
Напиши уравнение прямой ax+by+c=0, все точки которой находятся на равных расстояниях от точек A(2;3) и B(7;6).
Точки , которой находятся на равных расстояниях от точек A(2;3) и B(7;6) , лежат на серединном перпендикуляре к отрезку АВ.
Мусть произвольная точка имеет координаты М(х;у) . Тогда МА=МВ.
По формуле расстояния между двумя точками ищем длины отрезков
МА=√((2-х)²+(3-у)²) , МВ=√((7-х)²+(6-у)²). МА²=МВ² , тогда
(2-х)²+(3-у)²=(7-х)²+(6-у)²,
4-4х+х²+9-6у+у²=49-14х+х²+36-12у+у²,
10х+6у-72=0 или 5х+3у-36=0.
Формула расстояния между двумя точками
d=√( (х₁-х₂)²+(у₁-у₂)²+ (z₁-z₂)²), где (х₁;у₁; z₁), (х₂;у₂; z₂) -координаты концов отрезка.
orjabinina.
В треугольнике ABC PK-средняя линия треугольника,параллельная AB, P (2;3), K (-1;2) и С(0;0). Напишите уравнение прямой,содержащей сторону AB.
Объяснение:
Уравнение прямой у=кх+b . Ищем числа а,b.
1) РК-средняя линия ⇒ РК║АВ. У параллельных прямых одинаковое к. Ищем к прямой РК.
P (2;3), {3=2k+b
K (-1;2), {2=-1k+b. Вычтем из первого уравнения второе , получим 1=3k,k=1/3. Такое же k будет у прямой АВ.
2)Найдем координаты точки А, используя формулу середины отрезка, тк РК-средняя линия.
3)Составляем уравнение прямой у=кх+b ,содержащей сторону AB используя k=1/3 ,A(4;6).
6=1/3*4+b => b=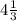
. Тогда 
.
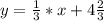orjabinina
Напиши уравнение прямой ax+by+c=0, все точки которой находятся на равных расстояниях от точек A(2;3) и B(7;6).
Объяснение:
Точки , которой находятся на равных расстояниях от точек A(2;3) и B(7;6) , лежат на серединном перпендикуляре к отрезку АВ.
Мусть произвольная точка имеет координаты М(х;у) . Тогда МА=МВ.
По формуле расстояния между двумя точками ищем длины отрезков
МА=√((2-х)²+(3-у)²) , МВ=√((7-х)²+(6-у)²). МА²=МВ² , тогда
(2-х)²+(3-у)²=(7-х)²+(6-у)²,
4-4х+х²+9-6у+у²=49-14х+х²+36-12у+у²,
10х+6у-72=0 или 5х+3у-36=0.
Формула расстояния между двумя точками
d=√( (х₁-х₂)²+(у₁-у₂)²+ (z₁-z₂)²), где (х₁;у₁; z₁), (х₂;у₂; z₂) -координаты концов отрезка.
orjabinina.