Один з кутів опуклого п'ятикутника дорівнює 115° другий третій і четвертий відносятся як 7:5:3 а пятий доровнює піврізниці другого. і четвертий кутів знайти невідомий кут
Найдем, как связаны радиусы вписанных окружностей.
Пусть сторона правильного треугольника равна a.
Сначала нужно найти длину отрезка AD. Проще всего это сделать по теореме косинусов.
Посмотрим на треугольник ABD. В нем BD = 7/15 a, AB = a, угол B = 60 градусов.
Тогда ,
AD = 13/15 a
Периметр треугольника ACD = a + 8/15 a + 13/15 a = 36/15 a, треугольника ABD = a + 7/15 a + 13/15 a = 35/15 a.
С одной стороны, площадь треугольника - половина прооизведения высоты на сторону, с другой - половина произведения периметра на радиус списанной окружности. Если считать по первой формуле, получим, что S1/S2 = CD/DB = 8/7 (здесь индекс 1 соответствует треугольнику ACD). По второй: S1/S2 = (36*r1)/(35*r2).
Итак,
Площади кругов пропорциональны квадратам радиусов, поэтому площади относятся как 100 к 81.
Есдиственный вопрос, площадь какого из кругов дана. Отсюда и 2 ответа: 81*100/81=100 или 81*81/100=65.61
Треугольник ba1c1 - равносторонний, все углы в нем 60 градусов.
Это все решение (причем самое полное и точное из всех). Но можно не останавливаться на достигнутом, и соединить вершины этого треугольника с вершиной куба d. Получается пирамида, у которой все грани - равносторонние треугольники. То есть получился тетраэдр (или, если хотите, правильный тераэдр, хотя это уточнение и лишнее - тетраэдром называют именно правильную треугольную пирамиду с равными ребрами), вписаный в куб. Конечно же, можно и наоборот - для любого тетраэдра можно построить такой куб, что ребра тетраэдра будут диагоналями граней куба.
Следствия.
Во первых, скрещивающиеся ребра тетраэдра взаимно перпендикулярны (в данном случае, к примеру, bd перпендикулярно a1c1, поскольку a1c1 II ac, а ac и bd - диагонали квадрата abcd, точно также доказывается перпендикулярность остальных пар скрещивающихся ребер тетраэдра).
Во вторых, отрезок, соединяющий середины скрещивающихся ребер тетраэдра, перпендикулярен этим ребрам и равен длине ребра тетраэдра, умноженной на √2/2. В самом деле, это отрезок, соединяющий центры противоположных граней куба, то есть он равен стороне куба, а ребро тетраэдра равно диагонали грани куба, откуда и получатеся соотношение длин.
Конечно, к задаче это имеет косвенное отношение (точнее, не имеет ни какого), но уж больно неприятно выдавать решение, занимающее полстрочки.
Найдем, как связаны радиусы вписанных окружностей.
Пусть сторона правильного треугольника равна a.
Сначала нужно найти длину отрезка AD. Проще всего это сделать по теореме косинусов.
Посмотрим на треугольник ABD. В нем BD = 7/15 a, AB = a, угол B = 60 градусов.
Тогда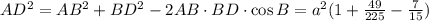 ,
,
AD = 13/15 a
Периметр треугольника ACD = a + 8/15 a + 13/15 a = 36/15 a, треугольника ABD = a + 7/15 a + 13/15 a = 35/15 a.
С одной стороны, площадь треугольника - половина прооизведения высоты на сторону, с другой - половина произведения периметра на радиус списанной окружности. Если считать по первой формуле, получим, что S1/S2 = CD/DB = 8/7 (здесь индекс 1 соответствует треугольнику ACD). По второй: S1/S2 = (36*r1)/(35*r2).
Итак,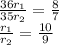
Площади кругов пропорциональны квадратам радиусов, поэтому площади относятся как 100 к 81.
Есдиственный вопрос, площадь какого из кругов дана. Отсюда и 2 ответа: 81*100/81=100 или 81*81/100=65.61
ответ: 100 или 65,61.
Треугольник ba1c1 - равносторонний, все углы в нем 60 градусов.
Это все решение (причем самое полное и точное из всех). Но можно не останавливаться на достигнутом, и соединить вершины этого треугольника с вершиной куба d. Получается пирамида, у которой все грани - равносторонние треугольники. То есть получился тетраэдр (или, если хотите, правильный тераэдр, хотя это уточнение и лишнее - тетраэдром называют именно правильную треугольную пирамиду с равными ребрами), вписаный в куб. Конечно же, можно и наоборот - для любого тетраэдра можно построить такой куб, что ребра тетраэдра будут диагоналями граней куба.
Следствия.
Во первых, скрещивающиеся ребра тетраэдра взаимно перпендикулярны (в данном случае, к примеру, bd перпендикулярно a1c1, поскольку a1c1 II ac, а ac и bd - диагонали квадрата abcd, точно также доказывается перпендикулярность остальных пар скрещивающихся ребер тетраэдра).
Во вторых, отрезок, соединяющий середины скрещивающихся ребер тетраэдра, перпендикулярен этим ребрам и равен длине ребра тетраэдра, умноженной на √2/2. В самом деле, это отрезок, соединяющий центры противоположных граней куба, то есть он равен стороне куба, а ребро тетраэдра равно диагонали грани куба, откуда и получатеся соотношение длин.
Конечно, к задаче это имеет косвенное отношение (точнее, не имеет ни какого), но уж больно неприятно выдавать решение, занимающее полстрочки.