дв -бисектриса и медиана, потому что треуг. равнобедреный. ев= (26-2х)/2=13-х
дв=20-х-(13-х)=7см
Если не понятно то вот ещё
обозначим вк медиану к ас. она же будет и высотой в треугольнике авс, поскольку он равнобедренный. медианы делятся в точке пересечения в отношении 2/1, считая от вершины.по условию во=24, тогда ок=12. по теореме пифагора ак=корень из(аоквадрат-окквадрат)=корень из(162-144)=3корня из 2.тогда основание ас=2*ак=6 корней из 2. обозначим mn отрезок l. треугольники мвn и авс подобны поскольку мn параллельна ас. тогда мn/во=ас/вк. мn/24=(6 корней из 2)/36, отсода искомая длина l=мn=4 корня из 2.
Площадь равнобедренной трапеции ABCD равна 48 см². Высота трапеции равна 4√3 см ,боковая сторона 5√3 см .Боковые стороны AB и CD продолжили до пересечения в точке О .Найдите площадь треугольника AOD в ( у см² ).
Объяснение:
1) Пусть МВ⊥АД, СР⊥АД. Тогда ΔАВМ=ΔДСР как прямоугольные по гипотенузе (АВ=СД) и острому углу (∠А=∠Д , как углы при основании равнобедренной трапеции)⇒ АМ=РД .
2)ΔАВМ-прямоугольный , по т. Пифагора АМ=√(25*3-16*3)=3√3 (см), значит РД=3√3 см.
боковые стороны по хсм,х+х+се=26
се=26-2х
дв -бисектриса и медиана, потому что треуг. равнобедреный. ев= (26-2х)/2=13-х
дв=20-х-(13-х)=7см
Если не понятно то вот ещё
обозначим вк медиану к ас. она же будет и высотой в треугольнике авс, поскольку он равнобедренный. медианы делятся в точке пересечения в отношении 2/1, считая от вершины.по условию во=24, тогда ок=12. по теореме пифагора ак=корень из(аоквадрат-окквадрат)=корень из(162-144)=3корня из 2.тогда основание ас=2*ак=6 корней из 2. обозначим mn отрезок l. треугольники мвn и авс подобны поскольку мn параллельна ас. тогда мn/во=ас/вк. мn/24=(6 корней из 2)/36, отсода искомая длина l=мn=4 корня из 2.
Площадь равнобедренной трапеции ABCD равна 48 см². Высота трапеции равна 4√3 см ,боковая сторона 5√3 см .Боковые стороны AB и CD продолжили до пересечения в точке О .Найдите площадь треугольника AOD в ( у см² ).
Объяснение:
1) Пусть МВ⊥АД, СР⊥АД. Тогда ΔАВМ=ΔДСР как прямоугольные по гипотенузе (АВ=СД) и острому углу (∠А=∠Д , как углы при основании равнобедренной трапеции)⇒ АМ=РД .
2)ΔАВМ-прямоугольный , по т. Пифагора АМ=√(25*3-16*3)=3√3 (см), значит РД=3√3 см.
3)Длина АД=АМ+МР+РД=6√3+МР . Пусть МН=у, АД=6√3+2у ⇒ВС=6√3+2у .
S(трап)=1/2*(АД+ВС)*ЕН , 48=1/2*(6√3+4у)*4√3 ,6√3+4у=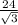 ,
,
4у= 8√3-6√3 , у=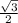 ⇒ ВЕ=
⇒ ВЕ=
4) АН=3√3-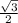 =3,5√3 (см).
=3,5√3 (см).
ΔОВЕ подобен ΔОАН по двум углам: ∠О-общий,∠ВЕО=∠АНО=90°, значит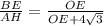 ,
, 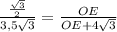 ,
, 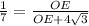 ,
,
OE=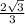 см
см
5) Высота ОН=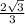 +4√3 =
+4√3 = 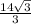 (см) , АД=6√3+√3=7√3 (см).
(см) , АД=6√3+√3=7√3 (см).
S(AOД)=1/2*АД*ОН , S(AOД=1/2* 7√3*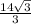 = 49(см²).
= 49(см²).