Одна із сторін AE правильного п'ятикутника ABCDE знаходиться на площині a, інша - поза площиною a. Чи будуть серед сторін цього пятикутника такі, які були б паралельні площині a?
Теорема . три высоты любого треугольника пересекаются в одной точке. доказательство: пусть abc - данный треугольник . пусть прямые, содержащие высоты ap и bq треугольника abc пересекаются в точке o. проведем через точку a прямую, параллельную отрезку bc, через точку b прямую, параллельную отрезку ac, а через точку c - прямую, параллельную отрезку ab. все эти прямые попарно пересекаются. пусть точка пересечения прямых, параллельных сторонам ac и bc - точка m, точка пересечения прямых, параллельных сторонам ab и bc - точка l, а прямых, параллельным ab и ac - точка k. точки klm не лежат на одной прямой, (иначе бы прямая ml совпадала бы с прямой mk, а значит, прямая bc была бы параллельна прямой ac, или совпадала бы с ней, то есть точки a, b и c лежали бы на одной прямой, что противоречит определению треугольника) . итак, точки k, l, m составляют треугольник. ma параллельно bc, и mb параллельно ac по построению. а значит, четырёхугольник macb - параллелограмм. следовательно, ma = bc, mb = ac. аналогично al = bc = ma, bk = ac = mb, kc = ab = cl. значит, ap и bq - серединные перпендикуляры к сторонам треугольника klm. они пересекаются в точке o, а значит, co - тоже срединный перпендикуляр. co перпендикулярно kl, kl параллельно ab, а значит co перпендикулярно ab. пусть r - точка пересечения ab и cq. тогда cr перпендикулярно ab, то есть cr - это высота треугольника abc. точка o принадлежит всем прямым, содержащим высоты треугольника abc. значит, прямые, содержащие высоты этого треугольника пересекаются в одной точке. что и требовалось доказать.
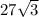 ед².
ед².
Объяснение:Обозначим данную пирамиду буквами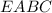 .
.
Проведём высоту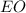 . Точка
. Точка 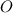 - центр
- центр 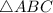 - точка пересечения, медиан, высот и биссектрис треугольника.
- точка пересечения, медиан, высот и биссектрис треугольника.
Проведём апофему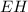 (апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне
(апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне 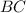 основания пирамиды.
основания пирамиды.
Т.к. данная пирамида - правильная, треугольная ⇒ основание пирамиды - правильный треугольник.
Проведём высоту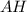 в
в 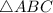 .
.
Т.к.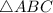 - равносторонний ⇒
- равносторонний ⇒ 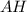 - высота, медиана, биссектриса.
- высота, медиана, биссектриса.
Высота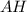 и апофема
и апофема 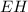 имеют общее основание, а именно точку
имеют общее основание, а именно точку 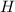 , т.к.
, т.к. 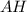 - медиана, а апофема
- медиана, а апофема 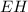 делит
делит 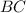 пополам (по свойству).
пополам (по свойству).
Рассмотрим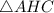 :
:
Найдём высоту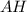 по теореме Пифагора:
по теореме Пифагора: 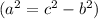
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Точка O - пересечение медиан и делит их в отношении 2 : 1, считая от вершины.
Рассмотрим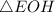 :
:
Если угол прямоугольного треугольника равен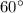 , то напротив лежащий катет равен произведению меньшего катета на
, то напротив лежащий катет равен произведению меньшего катета на 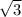 .
.
Найдём апофему по теореме Пифагора: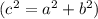
====================================================
⇒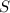 бок. поверх. =
бок. поверх. = 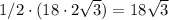 ед².
ед².
⇒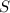 полн. поверх. =
полн. поверх. = 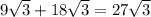 ед².
ед².