Около остроугольного треугольника авс описана окружность с центром о. ан высота этого треугольника. ав=15,ас=16, 5ан=6ао. найдите площадь треугольника оас.
Проведём ON ⊥ AC ⇒ ON - биссектриса и медиана равнобедренного треугольника AOC, тогда ∠AON = 0.5∠AOC. Так как ∠ABC - вписанный, то он равен половине центрального угла АОС, т.е. ∠ABC = 0.5∠AOC ⇒ ∠AON = ∠ABC, следовательно, ΔAON ~ ΔABH (по двум углам). Из подобия треугольников следует, что
Из прямоугольного треугольника AON по теореме Пифагора
решение представлено на фото
Проведём ON ⊥ AC ⇒ ON - биссектриса и медиана равнобедренного треугольника AOC, тогда ∠AON = 0.5∠AOC. Так как ∠ABC - вписанный, то он равен половине центрального угла АОС, т.е. ∠ABC = 0.5∠AOC ⇒ ∠AON = ∠ABC, следовательно, ΔAON ~ ΔABH (по двум углам). Из подобия треугольников следует, что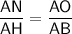
Из прямоугольного треугольника AON по теореме Пифагора
Площадь треугольника AOC:
ответ: 48 кв. ед.