Окружность вписана в ромб abcd, касаеться сторон cd и bc в точках m и q соответственно. прямая am и bc пересекаються в точке p.а) докажите, что bp*bq=bc^2b) найдите угол apc, если dm=1, mc=4
1)Радиус шара, вписанного в куб, равен половине ребра куба Верно, шар касается параллельных плоскостей куба в точках, которые лежат на перпендикулярных прямых, т.е. эти две точки образуют диаметр. 2)Радиус окружности, вписанной в ромб, равен половине меньшей диагонали ромба Неверно, Радиус вписанной окружности ромба, равен высоте из центра окружности или корню из произведения сторон, на которые высота разбивает основание 3) Радиус шара, вписанного в конус, равен половине высоты конуса Неверно, радиус шара равен (AH-AG)/2 где AH - высота конуса, а AG - отрезок высоты с точкой G, лежащей на окружности шара Вокруг любой четырёхугольной пирамиды можно описать конус Верно, если все боковые ребра пирамиды равны,то вокруг пирамиды можно описать конус (Четырёхугольная пирамида имеет равные боковые ребра)
Первое и четвёртое утверждение
Объяснение:
1)Радиус шара, вписанного в куб, равен половине ребра куба
Верно, шар касается параллельных плоскостей куба в точках, которые лежат на перпендикулярных прямых, т.е. эти две точки образуют диаметр.
2)Радиус окружности, вписанной в ромб, равен половине меньшей диагонали ромба
Неверно, Радиус вписанной окружности ромба, равен высоте из центра окружности или корню из произведения сторон, на которые высота разбивает основание
3) Радиус шара, вписанного в конус, равен половине высоты конуса
Неверно, радиус шара равен (AH-AG)/2 где AH - высота конуса, а AG - отрезок высоты с точкой G, лежащей на окружности шара
Вокруг любой четырёхугольной пирамиды можно описать конус
Верно, если все боковые ребра пирамиды равны,то вокруг пирамиды можно описать конус (Четырёхугольная пирамида имеет равные боковые ребра)
Расстояние от точки K до прямой MN - отрезок FK, равный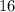 (см).
(см).
Объяснение:
1. Рассмотрим равносторонний ΔMNK:
Т.к. ΔMNK - равносторонний, то каждый угол будет равняться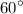 .
.
По условию из точки K к отрезку MN проведём биссектрису KF, которая по свойству делит ∠K на два равных угла.
⇒ ∠NKF = ∠FKM = 60° : 2 = 30°.
Расстояние от точки до прямой/отрезка - перпендикуляр.
⇒ Проводим из вершины F перпендикуляр к отрезку MK, равный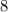 (см).
(см).
Благодаря этому перпендикуляру, получаем прямоугольный ΔFGK с прямым углом G (оставшиеся два угла - острые).
2. Рассмотрим прямоугольный ΔFGK:
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
⇒ катет FG в 2 раза меньше гипотенузы FK, т.е. FK =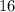 (см).
(см).
Т.к. ΔMNK - равносторонний ⇒ он является и равнобедренным с основанием NM.
Биссектриса, проведённая к основанию равнобедренного треугольника, является и высотой, и медианой.
⇒ биссектриса FK - высота треугольника MNK, и в тоже время перпендикуляр к прямой MN.
⇒ отрезок FK - расстояние от точки K до прямой MN.