Для начала найдем отношение ВР/РС. Для этого: Проведем BD параллельно АС. Тогда <PAC=<BDA, как накрест лежащие при параллельных прямых BD и AC и секущей АD. ∆АКМ ~ ∆BKD по двум углам (1). ∆АРС ~ ∆DРВ по двум углам (2). Из (1) BD/AM=4 и BD=4AM = 2AC. Из (2) BP/PC=2. ВМ - медиана и по ее свойствам Sabm=Scbm. Треугольники АВК и АКМ - треугольники с общей высотой к стороне ВМ. Значит Sabk/Sakm=4/1. => Sabk=Sabc*(1/2)*(4/5)=(2/5)*Sabc. Sakm=Sabc*1/(2*5)=(1/10)*Sabc. Треугольники ABP и APC - треугольники с общей высотой к стороне ВC. Значит Sabp/Sapc=2/1. => Sapc=Sabc*1/3=(1/3)*Sabc. Тогда Skpcm=Sapc-Sakm = (1/3)*Sabc-(1/10)*Sabc = (7/30)*Sabc. Sabk/Skpcm=(2/5)/(7/30)=12/7.
В треугольнике DFR провели прямую, параллельную стороне FR так, что она пересекает стороны DF и DR в точках S и Q, соответственно. Найди длину стороны DR, если площадь треугольника DSQ равна 42 см², SQ = 7 см, DS = 15 см, FR = 14 см.
4√37 см
Объяснение:
∠DSQ = ∠DFR как соответственные при пересечении SQ║FR секущей DF, ∠D - общий для треугольников DSQ и DFR, значит
ΔDSQ ~ ΔDFR по двум углам.
см
Отношение площадей подобных треугольников равно квадрату отношения сходственных сторон.
см²
Площадь треугольника DFR можно вычислить так же по формуле:
Проведем BD параллельно АС. Тогда <PAC=<BDA, как накрест лежащие при параллельных прямых BD и AC и секущей АD.
∆АКМ ~ ∆BKD по двум углам (1).
∆АРС ~ ∆DРВ по двум углам (2).
Из (1) BD/AM=4 и BD=4AM = 2AC.
Из (2) BP/PC=2.
ВМ - медиана и по ее свойствам Sabm=Scbm.
Треугольники АВК и АКМ - треугольники с общей высотой к стороне ВМ. Значит Sabk/Sakm=4/1. => Sabk=Sabc*(1/2)*(4/5)=(2/5)*Sabc.
Sakm=Sabc*1/(2*5)=(1/10)*Sabc.
Треугольники ABP и APC - треугольники с общей высотой к стороне ВC.
Значит Sabp/Sapc=2/1. => Sapc=Sabc*1/3=(1/3)*Sabc.
Тогда Skpcm=Sapc-Sakm = (1/3)*Sabc-(1/10)*Sabc = (7/30)*Sabc.
Sabk/Skpcm=(2/5)/(7/30)=12/7.
В треугольнике DFR провели прямую, параллельную стороне FR так, что она пересекает стороны DF и DR в точках S и Q, соответственно. Найди длину стороны DR, если площадь треугольника DSQ равна 42 см², SQ = 7 см, DS = 15 см, FR = 14 см.
4√37 см
Объяснение:
∠DSQ = ∠DFR как соответственные при пересечении SQ║FR секущей DF, ∠D - общий для треугольников DSQ и DFR, значит
ΔDSQ ~ ΔDFR по двум углам.
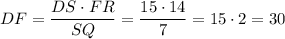 см
см
Отношение площадей подобных треугольников равно квадрату отношения сходственных сторон.Площадь треугольника DFR можно вычислить так же по формуле:
Из треугольника DFR по теореме косинусов:
DR² = 30² + 14² - 2 · 30 · 14 · 0,6
DR² = 900 + 196 - 504 = 592
DR = √592 = 4√37 см