Сечение цилиндра, проведенное параллельно его оси, находится на расстоянии 2 см от нее и является квадратом. Площадь боковой поверхности цилиндра равна 8√3π см2 . Найдите площадь сечения.
Объяснение:
S( бок цилиндра)=2πrh, где , r — радиус основания цилиндра, h — высота цилиндра. Тогда 8√3π=2πrh или 4√3=rh . Возведем обе части в квадрат( зачем? пригодится) (4√3)²=r²h ² , 48=r²h² (*) .
В сечении -квадрат АВСК. Причем АВ=BC=h. Площадь сечения S(квадрата)=BC²=h².Используя (*) h²=S=48:r² .
Т.к. сечение цилиндра, проведенное параллельно его оси, находится на расстоянии 2 см , то ОМ⊥ВС , ОМ=2 см.
ΔВСО-равнобедренный и ОМ-высота , а значит медиана . Тогда
Сечение цилиндра, проведенное параллельно его оси, находится на расстоянии 2 см от нее и является квадратом. Площадь боковой поверхности цилиндра равна 8√3π см2 . Найдите площадь сечения.
Объяснение:
S( бок цилиндра)=2πrh, где , r — радиус основания цилиндра, h — высота цилиндра. Тогда 8√3π=2πrh или 4√3=rh . Возведем обе части в квадрат( зачем? пригодится) (4√3)²=r²h ² , 48=r²h² (*) .
В сечении -квадрат АВСК. Причем АВ=BC=h. Площадь сечения S(квадрата)=BC²=h².Используя (*) h²=S=48:r² .
Т.к. сечение цилиндра, проведенное параллельно его оси, находится на расстоянии 2 см , то ОМ⊥ВС , ОМ=2 см.
ΔВСО-равнобедренный и ОМ-высота , а значит медиана . Тогда
ВМ=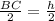
.
ΔВМО-прямоугольный по т. Пифагора r²=2²+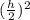
или
r²=4+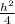
или r²=
.
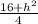S=48 :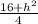
= 
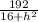(см²)
1) 15.2, 2) 10, 3) 24
Объяснение:
1) В прямоугольном треугольнике сторона, которая лежит напротив угла 30 градусов = половине гипотенузы, то есть:
0.5*CK=OK
CK=2*OK
CK = 2*7.6
CK = 15.2
2) Допустим дан треугольник со сторонами ABC и высотой AK, AB=AC, AK=5 см
Так как сумма углов треугольника равна 180°, то
∠ВАС = ∠ВСА = (180° - 120°) : 2 = 60° : 2 = 30°.
АK - катет, лежащий напротив угла 30°, значит он равен половине гипотенузы.
АС = 2 · АK = 2 · 5 = 10 см.
3) По той же схеме, что и в первом, напротив меньшего угла - меньшая сторона, по-этому:
x+2x=36
3x=36
x=36/3
x=12 - Катет
x*2=24 - Гипотенуза