Основание пирамиды мавс - треугольник авс, угол асв=90°, угол вас=60°, ас=4√3, боковая грань вмс перпендикулярна плоскости основания, две другие боковые грани наклонены к плоскости основания под углом 30°. найдите длину ребра мс. (в ответ - величина мс√3)

Показать ответ

Ответ:

leramoisejenko

16.03.2021 14:45

36см²

Объяснение:

Правильная треугольная пирамида - это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания. Значит треугольники которые образуют боковую поверхность являются равнобедренными.

Sбок.пов.=3*Sтреуг.=3*1/2*H*a

где H - это высота треугольника боковой поверхности.

а - длина основания треугольника боковой поверхности...

т.к. у нас имеется радиус r круга вписанного в основание, найдем величину а,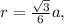 $r=\frac{\sqrt{3} }{6} a,$ , значит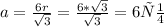 $a=\frac{6r}{\sqrt{3} }=\frac{6*\sqrt{3} }{\sqrt{3} } =6см$

Зная высоты пирамиды h из прямоугольного треугольника со сторонами r, h и H, найдем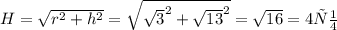 $H=\sqrt{r^{2}+h^{2} } =\sqrt{\sqrt{3} ^{2}+\sqrt{13} ^{2} }=\sqrt{16} =4см$

отсюда Sбок.пов.=3*Sтреуг.=3*1/2*H*a=3*1/2*4*6=36см²

0,0(0 оценок)

Ответ:

apiloota

08.02.2022 14:22

Две другие стороны треугольника равны по 30 см

Объяснение:

Если два внешних угла при различных вершинах равны между собой, это значит, что внутренние углы при этих вершинах также равны между собой, и треугольник равнобедренный.

1) Пусть основание треугольника равно а = 18 см, тогда боковая сторона равна b = 0,5 · (Р - а) = 0,5 · (78 - 18) = 30 (см)

2) Пусть боковые сторона равны по 18 см, то есть b = 18 см, тогда основание равно а = Р - 2b = 78 - 2 · 18 = 42 (см)

В этом случае не выполняется неравенство треугольника а < 2b потому что 42 > 36.

Видим, что таким решение быть не может

0,0(0 оценок)

Популярные вопросы: Геометрия