Основание представляет собой прямоугольную трапецию ABCD, нарисованную вне круга.
Вертикальная призма 5 см к боковым стенкам и высотой 3 см. Боковая стенка призмы 2 см. Найдите основание и площадь боковой поверхности призмы
Найдите площади поверхности
Проведём от точки N к точке P отрезок PN и от точки M к точке O отрезок MO так, что MN - часть средней линии данной трапеции. Соответственно, исходя из этого условия и зная длины BC и AD найдём длину отрезка PO.
Вернёмся к условию задачи. M и N — СЕРЕДИННЫЕ точки диагоналей AC и BD трапеции ABCD. И следовательно из ранее сказанной записи "MN - часть средней линии данной трапеции" мы можем сказать, что PN и MO равны сумме BC.
Поскольку нам известен отрезок, на котором находится искомый отрезок MN и два составляющих по бокам отрезка PO, то найдём отрезок MN.
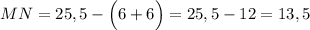 (см)
(см)
ответ:Площадь параллелограмма равна произведению основания на высоту:
В равнобедренном треугольника высота, проведённая к основанию, является медианой и биссектрисой.
По теореме Пифагора (рассматривается треугольник, образованный высотой, а не весь равнобедренный треугольник):
Тогда
Площадь треугольника равна половине произведения основания на высоту:
Т.к. площади треугольника и параллелограмма равны, то
ответ: 2.