Диагональ трапеции делит её на два подобных между собой треугольника. Отношение боковых сторон трапеции равно 2. Найдите отношение большего основания трапеции к её меньшему основанию.
РЕШЕНИЕ: Пусть в трапеции ABCD такой диагональю является BD. Тогда накрест лежащие углы CBD и ADВ равны.
Так как в трапеции противолежащие углы не равны, то другие пары равных углов это ABD=BCD и BAD=BDC.
Отношение пропорциональных сторон: АВ/CD=AD/BD=BD/BC=2
Поскольку фокусы гиперболы лежат на оси абсцисс симметрично относительно начала координат, то это стандартная гипербола, которая имеет уравнение:
Поскольку дана точка гиперболы, то подставим ее координаты в уравнение:
Также распишем эксцентриситет гиперболы:
Преобразуем. Возведем в квадрат:
Подставим в уравнение с координатами выявленное соотношение:
Все необходимые данные для записи уравнения есть:
Поскольку квадрат мнимой полуоси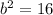
, то ее длина - соответственно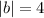 
18_03_09_Задание № 7:
Диагональ трапеции делит её на два подобных между собой треугольника. Отношение боковых сторон трапеции равно 2. Найдите отношение большего основания трапеции к её меньшему основанию.
РЕШЕНИЕ: Пусть в трапеции ABCD такой диагональю является BD. Тогда накрест лежащие углы CBD и ADВ равны.
Так как в трапеции противолежащие углы не равны, то другие пары равных углов это ABD=BCD и BAD=BDC.
Отношение пропорциональных сторон: АВ/CD=AD/BD=BD/BC=2
Выразим из второй части: AD/BD=2, AD=2BD
Выразим из третьей части: BD/BC=2, BD=2BC
Подставляем: AD=2*2BC=4BC. Значит AD/BC=4.
ОТВЕТ: 4:1