Назовем треугольник АВСД и точку пересечения диагоналей - О. Угол А = углу С = 120 градусов(по свойству ромба), тогда угол В = углу Д = 1/2(360-2*120) = 60 градусов.
В треугольнике АОВ угол ВАО = 1/2*А=1/2*120 = 60 градусов, а угол АВО = 1/2*В = 1/2*60 = 30 градусов.
АО = 1/2а, т.к. лежит против угла в 30 градусов в прямоугольном треугольнике АВО(угол АОВ=90, по свойству диагоналей ромба).
Отсюда, диагональ АС = 2*АО = 2* 1/2а = а (по свойству диагоналей ромба).
По теореме Пифагора ВО^2=AB^2-AO^2= a^2 - 1/4a^2, значит, ВО = (Корень квадратный из трех, деленный на два, умноженный на а).
Предложенное решение - полный бред!
Не настаиваю, что мое верное, но предлагаю свое.
1.После построения высоты МО=6 см получаем прямоугольный треугольник МОР с большим катетом МО и прилежащим углом ОМР=30 гр
Гипотенуза МР исходя из формулы равна
ОМ=МР*соs 30 гр
МР(гипотенуза) = ОМ:соs 30 гр = 6 : (кв к 3):2 = 12 : кв к 3
2. Треугольник равнобедренный, значит МР=РК = 12 : кв к 3
3. ОР - меньший катет в прямоугольном тр-ке, напротов угла в 30 гр, следовательно по формулам равен половине гипотенузы
ОР = МР:2 = 12:кв к 3 : 2 = 6: кв к 3 см
4. ОК = РК-ОР = 12: кв к 3 - 6: кв к 3 = (12-6) : кв к 3 = 6 : кв корень из 3 см
Назовем треугольник АВСД и точку пересечения диагоналей - О. Угол А = углу С = 120 градусов(по свойству ромба), тогда угол В = углу Д = 1/2(360-2*120) = 60 градусов.
В треугольнике АОВ угол ВАО = 1/2*А=1/2*120 = 60 градусов, а угол АВО = 1/2*В = 1/2*60 = 30 градусов.
АО = 1/2а, т.к. лежит против угла в 30 градусов в прямоугольном треугольнике АВО(угол АОВ=90, по свойству диагоналей ромба).
Отсюда, диагональ АС = 2*АО = 2* 1/2а = а (по свойству диагоналей ромба).
По теореме Пифагора ВО^2=AB^2-AO^2= a^2 - 1/4a^2, значит, ВО =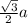
(Корень квадратный из трех, деленный на два, умноженный на а).
Следовательно, ВД = 2*ВО = 2 *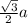
= 
.
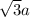ответ: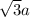
(Корень из трех, умноженный на а).