Основанием четырехугольной пирамиды является ромб с острым углом 30, а все боковые грани пирамиды наклонены к основанию под углом 60...

Основанием четырехугольной пирамиды является ромб с острым углом 30, а все боковые грани пирамиды на

Показать ответ

Ответ:

neznayka1900

15.02.2022 04:06

$\boxed{S_{b} = 2304}$ квадратных единиц

Объяснение:

Дано: KABCD - четырехугольная пирамида, ABCD - ромб, ∠ABC = 30°,

∠(KAB, ABC) = 60°, KO ⊥ ABC,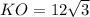 $KO = 12\sqrt{3}$ , AC ∩ BD = O

Найти: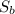 $S_{b}$ - ?

Решение: Из точки K проведем перпендикуляр на сторону AB в точку T, то есть KT ⊥ AB по построению. Соединим точки O и T, которые лежат в одной плоскости ABC, то есть прямая OT лежит в плоскости ABC по аксиоме стереометрии. Так как по условию KO ⊥ ABC, то по определению перпендикулярности прямой к плоскости KO перпендикулярно любой прямой лежащей в плоскости ABC, так как OT ⊂ ABC, то KO ⊥ OT. Треугольник ΔKOT - прямоугольный, так как KO ⊥ OT, тогда отрезок OT - проекция KT на плоскость ABC. По теореме о трех перпендикулярах OT ⊥ AB, так как KO ⊥ OT, KT ⊥ AB - по построению и отрезок OT - проекция KT на плоскость ABC из прямоугольного треугольника ΔKOT. Так как OT ⊥ AB по теореме о трех перпендикулярах и KT ⊥ AB - по построению, то угол ∠KTO - линейный угол двухгранного угла между плоскостями KAB и ABC, то есть угол ∠KTO = ∠(KAB, ABC) = 60°. Рассмотрим прямоугольный треугольник ΔKOT: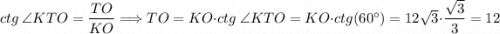 $ctg \ \angle KTO = \dfrac{TO}{KO} \Longrightarrow TO = KO \cdot ctg \ \angle KTO = KO \cdot ctg(60^{\circ}) = 12\sqrt{3} \cdot \dfrac{\sqrt{3} }{3} =12$ .

Так как по условию AC ∩ BD = O, то точка пересечения диагоналей - центр ромба и так как TO ⊥ AB, то отрезок OT - радиус окружности вписанной в ромб. По формуле площади ромба:

$S_{ABCD} = \dfrac{4\cdot TO^{2}}{\sin \angle ABC} = \dfrac{4 \cdot (12)^{2}}{\sin 30^{\circ}} = \dfrac{4 \cdot 144}{0,5} = 144 \cdot 8 = 1152$ квадратных единиц.