Основанием четырехугольной призмы служит прямоугольник со сторонами 12см и 16см. найти боковую поверхность и объем четырехугольной призмы, если ее высота равна 17см. решить, () контрольная

1. Координаты середины отрезка - полусумма координат начала и конца.
Значит С((2-2)/2;(2+2)/2) или С(0;2). ответ г).
3. Координаты вектора - разность координат конца и начала этого вектора.
АВ{-2-2;7-7} или AB{-4;0}.
4. Длина вектора а{6;-8} равна его модулю: |a|=√(6²+(-8)²)=10.
5. Чтобы проверить, лежит ли точка на окружности, надо подставить координаты точки в уравнение окружности:
(-5+5)²+(-3-1)²=16 или 0+16=16. ответ: а) да, лежит.
6. Длина радиуса этой окружности - модуль вектора М0.
|M0|=√(0-(-3))²+(0-4)²)=√(9+16)=5. ответ в)

2) x²+y²=5²

3)

A) центр окружности в точке (0;0), радиус окружности равен 4.

B) центр окружности в точке (3; -2), радиус окружности равен 5.

C) центр окружности в точке (0;0), радиус окружности равен 8.

D) центр окружности в точке (-1; 0), радиус окружности равен .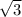

Объяснение:

2) Так как уравнение окружности проходит через начало координат, то это уравнение имеет вид: x²+y²=R². Теперь надо найти R². R равен ОА - как расстояние от центра окружности к точке А.

Вычисляем расстояние ОА по формуле расстояния между двумя точками. Нам даже нужно не ОА, а ОА².

ОА²=(0-(-3))²+(4-0)²

ОА²=9+16

ОА²=25.

Получаем x²+y²=5².

3)

А) Как уже замечали в предыдущей задаче центр данной окружности проходит через начало координат. Радиус равен .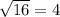

B) Уравнение окружности имеет вид:

(х-а)²+(y-b)²=R².

Здесь центром окружности будет (a, b), радиусом будет R.

Зная это, получим (3; -2) - центр этой окружности. .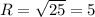

C) Перепишем уравнение в виде: x²+y²=64. Или x²+y²=8². Опять таки получили окружность с началом в центре координат, а радиус равен

R²=8². То есть R=8.

D) (x+1)²+y²=3. Центр окружности равен (-1; 0). Радиус окружности равен R²=3.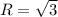

Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень