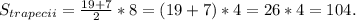Основанием прямой призмы является трапеция. Найти площадь сечения, проходящего через высоты оснований. Основания трапеции равны 2 и 8 см, боковые стороны основания 5 см.
Площадь равнобедренной трапеции равна полусумме оснований, умноженной на высоту.
Высота у нас уже есть Одно из оснований - тоже. Теперь надо найти большее основание. Если опустить высоту с меньшего основания на большее, то получим прямоугольный треугольник, где гипотенузой будет боковая сторона, одним из катетов - высота трапеции, а вторым катетом - часть основания трапеции. Чтобы узнать большее основание трапеции, нам нужно вычислить этот неизвестный катет в треугольнике, потому что длиной большего основания будет сумма двух таких катетов с меньшим основанием. Так как точно такой же треугольник можно получить, опустив высоту из другой точки меньшего основания трапеции. По теореме Пифагора вычисляем неизвестный катет . Значит длина наибольшего катета равна 7+6+6=19 см.
Площадь равнобедренной трапеции равна полусумме оснований, умноженной на высоту.
Высота у нас уже есть Одно из оснований - тоже. Теперь надо найти большее основание. Если опустить высоту с меньшего основания на большее, то получим прямоугольный треугольник, где гипотенузой будет боковая сторона, одним из катетов - высота трапеции, а вторым катетом - часть основания трапеции. Чтобы узнать большее основание трапеции, нам нужно вычислить этот неизвестный катет в треугольнике, потому что длиной большего основания будет сумма двух таких катетов с меньшим основанием. Так как точно такой же треугольник можно получить, опустив высоту из другой точки меньшего основания трапеции. По теореме Пифагора вычисляем неизвестный катет . Значит длина наибольшего катета равна 7+6+6=19 см.
Площадь равнобедренной трапеции равна полусумме оснований, умноженной на высоту.
Высота у нас уже есть Одно из оснований - тоже. Теперь надо найти большее основание. Если опустить высоту с меньшего основания на большее, то получим прямоугольный треугольник, где гипотенузой будет боковая сторона, одним из катетов - высота трапеции, а вторым катетом - часть основания трапеции. Чтобы узнать большее основание трапеции, нам нужно вычислить этот неизвестный катет в треугольнике, потому что длиной большего основания будет сумма двух таких катетов с меньшим основанием. Так как точно такой же треугольник можно получить, опустив высоту из другой точки меньшего основания трапеции. По теореме Пифагора вычисляем неизвестный катет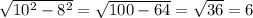
. Значит длина наибольшего катета равна 7+6+6=19 см.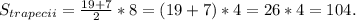 
Площадь равнобедренной трапеции равна полусумме оснований, умноженной на высоту.
Высота у нас уже есть Одно из оснований - тоже. Теперь надо найти большее основание. Если опустить высоту с меньшего основания на большее, то получим прямоугольный треугольник, где гипотенузой будет боковая сторона, одним из катетов - высота трапеции, а вторым катетом - часть основания трапеции. Чтобы узнать большее основание трапеции, нам нужно вычислить этот неизвестный катет в треугольнике, потому что длиной большего основания будет сумма двух таких катетов с меньшим основанием. Так как точно такой же треугольник можно получить, опустив высоту из другой точки меньшего основания трапеции. По теореме Пифагора вычисляем неизвестный катет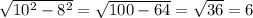
. Значит длина наибольшего катета равна 7+6+6=19 см. 