Основания биссектрис треугольника принадлежат плоскости α. принадлежат ли плоскости α вершины треугольника? ответ обоснуйте.

ответ: 1) 6.

2) 30°; 150°; 30° и 150°.

3) 300.

Объяснение: 1) S=ah

72=12h

h=72:12

h=6 (см.).

2) (Начерти ромб).

Ромб-это параллелограмм, у которого все стороны равны. Значит, формула нахождения площади, как у параллелограмма.

S=ah

98=7a

a=98:7

a=14.

Я уже говорила, что ромб-это параллелограмм, у которого все стороны равны. Значит, а=b=с=d=14.

Проведя высоту, можно заметить, что в образованном треугольнике гипотенуза больше катета в 2 раза. Следовательно, работает следующее правило: против ∠ в 30° лежит катет, равный половине гипотенузы. Значит, острый ∠ ромба=30°.

Тупой ∠ ромба=180°-30°=150°.

В ромбе противоположные углы равны⇒∠1=∠3=30°, ∠2=∠4=150°.

3) (Начерти трапецию).

Проведём высоту ВН и рассмотрим получившийся треугольник-прямоугольный, так как ВН-высота.

Острый угол трапеции равен 45°, а значит и острый угол получившегося треугольника равен 45°. Найдём оставшийся неизвестный угол треугольника. 90°-45°=45°. Острые углы прямоугольного треугольника равны, значит, треугольник равнобедренный⇒катет а=катету в (или высоте h).

a=h=(40-20):2=20:2=10.

S=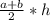

S=.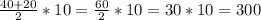

1)  150.

2)  15.

3)  18.

4)  270.

Объяснение:

Площадь трапеции определяется по формуле:

S=h(a+b)/2;  

1)  a=9+12=21;  b=4;   h=12.

S=12*(21+4)/2=6*25=150;

***

2)  S=h(a+b)/2;  a=3;  b=9;  h=?  Высота (катет )лежит против угла в 30* и равна половине гипотенузы h=5/2=2.5;

S=2.5(3+9)/2;

S=2.5*12/2;

S=2.5*6=15.

***

3)  Вероятно это равнобокая трапеция и углы при основаниях равны.

Проведем высоту из вершины тупого угла.  Получим равнобедренный треугольник с углами по 45*,  стороны которых (и высота) равны 9-2*3=9-6=3;

S=h(a+b)/2;  h=3;  a=3;  b=9;

S=3(3+9)/2=3*12/2=18.

***

4)  Все величины для нахождения площади известны.

S=h(a+b)/2;  h=15;  a=4;  b=8+24=32;

S=15(4+32)/2;

S=15*36*2=15*18=270.