Основания правильной усеченной треугольной пирамиды равны 1:2,а высота равна 6 см. Угол между боковым ребром и плоскостью основания равна 45°.Найди площади оснований.

Показать ответ

Ответ:

BackedSmile

08.11.2021 09:23

В соответствии с классическим определением, угол между векторами,отложенными от одной точки, определяется как кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором. Для заданного варианта углы между векторами могут быть определены из соотношения углов в треугольнике ABC, в котором ∠АСВ=90°, ∠СВА=40°, соответственно ∠САВ=180°-(90°+40°)=50°. Тогда -
- угол между векторами СА и СВ равен ∠АСВ=90°;
- угол между векторами ВА и СА равен ∠САВ=50°;
- угол между векторами СВ и ВА равен ∠САВ+∠АСВ=50°+90°=140°

0,0(0 оценок)

Ответ:

Katenkalovely

09.06.2021 08:07

ответ: а=4 .

ΔАВС - правильный ⇒ все его стороны равны "а" . Высота равностороннего треугольника является и медианой. Так как ОХ⊥ОУ , то если две вершины лежат на оси ОХ, тогда третья вершина лежит на оси ОУ. Пусть вершины А и С лежат на оси ОХ, тогда координаты точки А(х,0) , а координаты точки С(-х,0). Вершина В лежит на оси ОУ и её координаты будут В(0,у) .

По условию сумма всех координат равна:

(-х+0)+(х+0)+(0+у)=2√3 ⇒

у=2√3 (2√3>0 ⇒ точка В лежит в верхней полуплоскости) ⇒ высота ВО=h=2√3 .

По теореме Пифагора из прямоугольного ΔАВО имеем: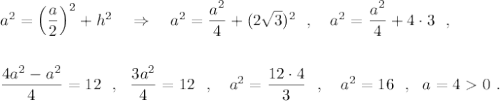 $a^2=\Big(\dfrac{a}{2}\Big)^2+h^2\ \ \ \Rightarrow \ \ \ a^2=\dfrac{a^2}{4}+(2\sqrt3)^2\ \ ,\ \ \ a^2=\dfrac{a^2}{4}+4\cdot 3\ \ ,\\\\\\\dfrac{4a^2-a^2}{4}=12\ \ ,\ \ \dfrac{3a^2}{4}=12\ \ ,\ \ \ a^2=\dfrac{12\cdot 4}{3}\ \ ,\ \ \ a^2=16\ \ ,\ \ a=40\ .$