Основания равнобокой трапеции относятся как 2:3, а диагональ делит ее острый угол пополам. Найдите боковую сторону этой трапеции, если её периметр равен 45 см.
Природа Аргентины обладает большим разнообразием от высокогорных Анд до обширных равнин, от субтропических лесов до ледников. Разнообразие, которым обладает природа этого государства, обусловлено большой территорией и разнообразным рельефом. Здешние пейзажи, флора и фауна привлекает туристов со всего мира. Аргентинская республика расположена на юго-западе Латинской Америки. На востоке страна омывается водами Атлантического океана. На юге находится остров Огненная Земля. Аргентине принадлежит восточная часть острова. Остров также омывается водами Атлантическим океана (Чилийская часть острова омывается Тихим океаном) а также проливом Дрейка на юге и Многоплановым проливом на севере. Крупнейшая река протекающая в стране - река Парана. Она занимает второе место по протяжности после Амазонки во всей Южной Америке. Река впадает в залив Атлантического океана Ла-Плата. Среди других больших рек: Уругвай, Рио-Негро, Рио-Колорадо. В Аргентине есть такие природные зоны как савана, степь, пустыня, субтропические леса. На севере находится природная зона саван под названием Гран-Чако, в центральной части расположена природная зона степи под названием Пампа, на юге расположена Патагония обширный край степных и пустынных земель. Самое известное чудо природы государства водопад Игуасу это чудо природы находится на границе с Бразилией.
Окружность, центр которой расположен в первой координатной четверти, касается оси Ox в точке M, пересекает две гиперболы y = и y = (k1, k2 > 0) в точках A и B таких, что прямая AB проходит через начало координат O. Известно, что k1 * k2 = 144. Найдите наименьшую возможную длину отрезка OM.В ответ запишите квадрат длины ОМ.
Объяснение:
Прямая АВ , проходящая через начало координат имеет вид у=кх
Найдем точки пересечения этой прямой и гипербол:
y = и у=кх → = кх , х²= ; x = ( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* .
y = и у=кх → = кх , х²= ; x = ( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* .
По свойство касательной и секущей проведенных из одной точки ОМ²=ОА*ОВ. Найдем ОА и ОВ по формулам расстояния между точками : ОА= = ,
ОB= = .
Тогда ОМ²= * = . Т.к ≥2 ,по следствию из неравенства о среднем арифметическом и среднем геометрическом , то принимает наименьшее значение равное 2 , а к1*к2=144, то ОМ²=2*√144=2*12=24.
===========================================
Свойство касательной и секущей проведенных из одной точки : "Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью."
Формула расстояния между точками d=√( (х₁-х₂)²+(у₁-у₂)² ), где (х₁;у₁ ), (х₂;у₂ ) -координаты концов отрезка.
Окружность, центр которой расположен в первой координатной четверти, касается оси Ox в точке M, пересекает две гиперболы y =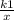 и y =
и y = 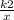 (k1, k2 > 0) в точках A и B таких, что прямая AB проходит через начало координат O. Известно, что k1 * k2 = 144. Найдите наименьшую возможную длину отрезка OM.В ответ запишите квадрат длины ОМ.
(k1, k2 > 0) в точках A и B таких, что прямая AB проходит через начало координат O. Известно, что k1 * k2 = 144. Найдите наименьшую возможную длину отрезка OM.В ответ запишите квадрат длины ОМ.
Объяснение:
Прямая АВ , проходящая через начало координат имеет вид у=кх
Найдем точки пересечения этой прямой и гипербол:
y =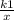 и у=кх →
и у=кх → 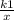 = кх , х²=
= кх , х²= 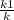 ; x =
; x = 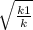 ( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к*
( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* 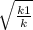 .
.
y =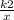 и у=кх →
и у=кх → 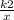 = кх , х²=
= кх , х²= 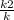 ; x =
; x = 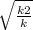 ( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к*
( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* 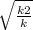 .
.
По свойство касательной и секущей проведенных из одной точки ОМ²=ОА*ОВ. Найдем ОА и ОВ по формулам расстояния между точками : ОА=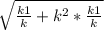 =
= 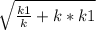 ,
,
ОB=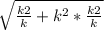 =
= 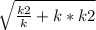 .
.
Тогда ОМ²=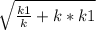 *
* 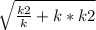 =
= 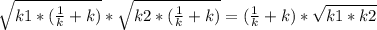 . Т.к
. Т.к 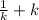 ≥2 ,по следствию из неравенства о среднем арифметическом и среднем геометрическом , то принимает наименьшее значение равное 2 , а к1*к2=144, то ОМ²=2*√144=2*12=24.
≥2 ,по следствию из неравенства о среднем арифметическом и среднем геометрическом , то принимает наименьшее значение равное 2 , а к1*к2=144, то ОМ²=2*√144=2*12=24.
===========================================
Свойство касательной и секущей проведенных из одной точки : "Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью."
Формула расстояния между точками d=√( (х₁-х₂)²+(у₁-у₂)² ), где (х₁;у₁ ), (х₂;у₂ ) -координаты концов отрезка.