Основаниями усеченной пирамиды служат равнобедренные прямоугольные треугольники, гипотенузы которых равны 7 см и 5 см. Найти объём усечённой пирамиды если её высота равно 12 см.
Высота правильной четырехугольной пирамиды равна v6 см, а боковое ребро наклонено к плоскости основания под углом б0 градусов. a) Найдите боковое ребро пирамиды б) Найдите площадь боковой поверхности пирамиды Пусть дана пирамида КАВСД. Пирамила правильная, поэтому основание -правильный четырехугольник - квадрат. Основанием высоты пирамиды является точка пересечения его диагоналей О. Все боковые ребра равны, их проекции равны половине диагонали квадрата. Т.к. боковые ребра равны, перпендикулярное сечение АКС пирамиды- равнобедренный треугольник. А т.к. угол при основании равен 60°, этот треугольник - равносторонний. Высота пирамиды КО-V6, и боковое ребро этого треугольника paBHO: AC=AK=CK=KO:sin(60°)=/6:((v3): 2}=2v2Площадь боковой поверхности пирамиды равна сумме площадейее граней, то есть половине произведения апофемы на периметр основания. Сторону основания найдем из прямоугольного треугольника АДС. Т.к. диагональ квадрата в основании равна 2V2, то его сторона равна 2. (Можно проверить по т.Пифагора). МО-ДС:231 Тогда апофема КМ из треугольника МОК равна по т.Пифагора v7см S 6oK-(4*2v7):2=4/7 cm?
A) центр окружности в точке (0;0), радиус окружности равен 4.
B) центр окружности в точке (3; -2), радиус окружности равен 5.
C) центр окружности в точке (0;0), радиус окружности равен 8.
D) центр окружности в точке (-1; 0), радиус окружности равен .
Объяснение:
2) Так как уравнение окружности проходит через начало координат, то это уравнение имеет вид: x²+y²=R². Теперь надо найти R². R равен ОА - как расстояние от центра окружности к точке А.
Вычисляем расстояние ОА по формуле расстояния между двумя точками. Нам даже нужно не ОА, а ОА².
ОА²=(0-(-3))²+(4-0)²
ОА²=9+16
ОА²=25.
Получаем x²+y²=5².
3)
А) Как уже замечали в предыдущей задаче центр данной окружности проходит через начало координат. Радиус равен .
B) Уравнение окружности имеет вид:
(х-а)²+(y-b)²=R².
Здесь центром окружности будет (a, b), радиусом будет R.
Зная это, получим (3; -2) - центр этой окружности. .
C) Перепишем уравнение в виде: x²+y²=64. Или x²+y²=8². Опять таки получили окружность с началом в центре координат, а радиус равен
Высота правильной четырехугольной пирамиды равна v6 см, а боковое ребро наклонено к плоскости основания под углом б0 градусов. a) Найдите боковое ребро пирамиды б) Найдите площадь боковой поверхности пирамиды Пусть дана пирамида КАВСД. Пирамила правильная, поэтому основание -правильный четырехугольник - квадрат. Основанием высоты пирамиды является точка пересечения его диагоналей О. Все боковые ребра равны, их проекции равны половине диагонали квадрата. Т.к. боковые ребра равны, перпендикулярное сечение АКС пирамиды- равнобедренный треугольник. А т.к. угол при основании равен 60°, этот треугольник - равносторонний. Высота пирамиды КО-V6, и боковое ребро этого треугольника paBHO: AC=AK=CK=KO:sin(60°)=/6:((v3): 2}=2v2Площадь боковой поверхности пирамиды равна сумме площадейее граней, то есть половине произведения апофемы на периметр основания. Сторону основания найдем из прямоугольного треугольника АДС. Т.к. диагональ квадрата в основании равна 2V2, то его сторона равна 2. (Можно проверить по т.Пифагора). МО-ДС:231 Тогда апофема КМ из треугольника МОК равна по т.Пифагора v7см S 6oK-(4*2v7):2=4/7 cm?
2) x²+y²=5²
3)
A) центр окружности в точке (0;0), радиус окружности равен 4.
B) центр окружности в точке (3; -2), радиус окружности равен 5.
C) центр окружности в точке (0;0), радиус окружности равен 8.
D) центр окружности в точке (-1; 0), радиус окружности равен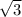 .
.
Объяснение:
2) Так как уравнение окружности проходит через начало координат, то это уравнение имеет вид: x²+y²=R². Теперь надо найти R². R равен ОА - как расстояние от центра окружности к точке А.
Вычисляем расстояние ОА по формуле расстояния между двумя точками. Нам даже нужно не ОА, а ОА².
ОА²=(0-(-3))²+(4-0)²
ОА²=9+16
ОА²=25.
Получаем x²+y²=5².
3)
А) Как уже замечали в предыдущей задаче центр данной окружности проходит через начало координат. Радиус равен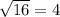 .
.
B) Уравнение окружности имеет вид:
(х-а)²+(y-b)²=R².
Здесь центром окружности будет (a, b), радиусом будет R.
Зная это, получим (3; -2) - центр этой окружности.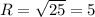 .
.
C) Перепишем уравнение в виде: x²+y²=64. Или x²+y²=8². Опять таки получили окружность с началом в центре координат, а радиус равен
R²=8². То есть R=8.
D) (x+1)²+y²=3. Центр окружности равен (-1; 0). Радиус окружности равен R²=3.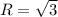
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень