Основи рівнобічної трапеції дорівнюють 8 см і 18 см. Через центр О кола, вписаного в цю трапецію, проведено перпендикуляр OK до площини трапеції, OK = 8 см. Знайдіть відстань від точки К до сторiн трапеції.
Найдём сначала третью сторону ΔАВС по теореме Пифагора
АС² + ВС² = АВ²
АС² = АВ² - ВС²
АС² = 8² - 4²
АС² = 64 - 16
АС² = 48
АС = √48 = 4√3
Высота прямоугольного треугольника, опущенная из вершины прямого угла вычисляется по формуле: h = , где а и в - катеты, с - гипотенуза
h = = 2
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом: h = , где х и у - это отрезки, на которые высота делит гипотенузу.
Пусть BD = х см, тогда АD = (8 - х) см.
Значит, СD =
CD² = BD . AD
(2√3)² = х · ( 8 - х )
х² - 8х + 12= 0
х = 2 или х = 6
Условию задачи удовлетворяет х=2 ( проверяем теорему Пифагора для ΔCBD).
Точка пересечения диагоналей параллелограмма делит их пополам, значит АО=ОС, BO=OD.
В тр-ке △АМС АМ=МС (из рисунка), значит △АМС - равнобедренный и поскольку АО=ОС, то МО медиана и высота.
В тр-ке △BMD BM=MD (из рисунка), значит △BMD - равнобедренный и поскольку BO=OD, то МО медиана и высота.
Таким образом, МО перпендикулярна и BD и АС, тогда по признаку: "Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости" следует, что МО⊥АВС чтд
ответ: 2 см
Объяснение:
Найдём сначала третью сторону ΔАВС по теореме Пифагора
АС² + ВС² = АВ²
АС² = АВ² - ВС²
АС² = 8² - 4²
АС² = 64 - 16
АС² = 48
АС = √48 = 4√3
Высота прямоугольного треугольника, опущенная из вершины прямого угла вычисляется по формуле: h =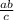
, где а и в - катеты, с - гипотенуза
h =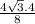
= 2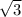
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом: h =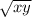
, где х и у - это отрезки, на которые высота делит гипотенузу.
Пусть BD = х см, тогда АD = (8 - х) см.
Значит, СD =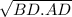
CD² = BD . AD
(2√3)² = х · ( 8 - х )
х² - 8х + 12= 0
х = 2 или х = 6
Условию задачи удовлетворяет х=2 ( проверяем теорему Пифагора для ΔCBD).
ответ : ВD = 2 см.
Значи
Объяснение:
Наугад взял: 2стр. 3й слева, где типа пирамиды.
Точка пересечения диагоналей параллелограмма делит их пополам, значит АО=ОС, BO=OD.
В тр-ке △АМС АМ=МС (из рисунка), значит △АМС - равнобедренный и поскольку АО=ОС, то МО медиана и высота.
В тр-ке △BMD BM=MD (из рисунка), значит △BMD - равнобедренный и поскольку BO=OD, то МО медиана и высота.
Таким образом, МО перпендикулярна и BD и АС, тогда по признаку: "Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости" следует, что МО⊥АВС чтд