Объяснение:
Дано: DO1 (R) =6 см, AO (r)=2 см, ∠ADA1=45°
Решение
Проведем высоту ОО1. Тогда AOO1D — прямоугольная трапеция. Проведем AA1⊥DO1. АОО1А1 — прямоугольник, так что AO=A1O1=r.
Тогда DA1=DO1-A1O1=R-r.
Далее, в прямоугольном треугольнике ΔDAA1 ∠ADA1=45°, так что ∠DAA1=90°-∠ADA1=45°. Поэтому ΔDAA1 — равнобедренный и прямоугольном треугольник.
Тогда DA1=AA1=H конуса=R-r=6-2=4
V= *π *H ( + (r*R)+)=*4*π(+(2*6)+)= *π см3
Чтоб найти S пов. сначала найдем твірну (L)
L===4 см
S пов.= π(r+R)*L+π+π=8π(+5)
В сечении - четырёхугольник АКТЕ, симметричный относительно диагонали АТ.
Применим теорему Менелая.
(СМ/ВМ)*(ВК/KS)*(ST/TC) = 1.
(6√2/3√2)*(BK/KS)*((3√2/2)/(3√2/2)) = 1.
Отсюда получаем отношение (BK/KS) = 1/2.
Тогда KS = (2/3)BS = (2/3)*(3√2) = 2√2.
Теперь в треугольнике STK имеем 2 стороны и знаем угол в 60 градусов. По теореме косинусов:
TK = √((3√2/2)² + (2√2)² - 2*(3√2/2)*(2√2)*cos 60) = √((9/2) + 8 - 6) = √(13/2).
Аналогично АК = √((√2)² + (3√2)² - 2*(√2)*(3√2)*cos 60) = √(2 + 18 - 6) = √14.
Отрезки ТЕ и ЕА равны √(13/2) и √14.
Сумма квадратов 2*(13/2) + 2*14 = 13 + 28 = 41.
Объяснение:
Дано: DO1 (R) =6 см, AO (r)=2 см, ∠ADA1=45°
Решение
Проведем высоту ОО1. Тогда AOO1D — прямоугольная трапеция. Проведем AA1⊥DO1. АОО1А1 — прямоугольник, так что AO=A1O1=r.
Тогда DA1=DO1-A1O1=R-r.
Далее, в прямоугольном треугольнике ΔDAA1 ∠ADA1=45°, так что ∠DAA1=90°-∠ADA1=45°. Поэтому ΔDAA1 — равнобедренный и прямоугольном треугольник.
Тогда DA1=AA1=H конуса=R-r=6-2=4
V=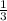 *π *H (
*π *H (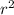 + (r*R)+
+ (r*R)+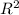 )=
)=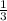 *4*π(
*4*π(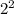 +(2*6)+
+(2*6)+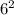 )=
)= 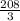 *π см3
*π см3
Чтоб найти S пов. сначала найдем твірну (L)
L=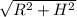 =
= =4
=4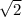 см
см
S пов.= π(r+R)*L+π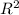 +π
+π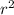 =8π(
=8π(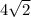 +5)
+5)
В сечении - четырёхугольник АКТЕ, симметричный относительно диагонали АТ.
Применим теорему Менелая.
(СМ/ВМ)*(ВК/KS)*(ST/TC) = 1.
(6√2/3√2)*(BK/KS)*((3√2/2)/(3√2/2)) = 1.
Отсюда получаем отношение (BK/KS) = 1/2.
Тогда KS = (2/3)BS = (2/3)*(3√2) = 2√2.
Теперь в треугольнике STK имеем 2 стороны и знаем угол в 60 градусов. По теореме косинусов:
TK = √((3√2/2)² + (2√2)² - 2*(3√2/2)*(2√2)*cos 60) = √((9/2) + 8 - 6) = √(13/2).
Аналогично АК = √((√2)² + (3√2)² - 2*(√2)*(3√2)*cos 60) = √(2 + 18 - 6) = √14.
Отрезки ТЕ и ЕА равны √(13/2) и √14.
Сумма квадратов 2*(13/2) + 2*14 = 13 + 28 = 41.