Основою прямої призми є прямокутний трикутник авс. ас=12 см, ав=13 см. висота призми дорівнює найменшій стороні її основи.
1)знайдіть довжину бічного ребра цієї призми.
2)знайдіть площу повної поверхні цієї призми​

Объяснение:

1)  Вектор  3a - b = 3•{ 5 ; 0 ;- 2 } - { 1 ; 2 ; 1 } = { 15 ; 0 ;- 6 } - { 1 ; 2 ; 1 } =

     = { 14 ;- 2 ;- 7 } ;    3a - b =  { 14 ;- 2 ;- 7 } .

2) Вектор  3a + 2b = 3•{ 2 ; 2 ; 1 } + 2•{ 3 ;- 2 ; 1 } = { 6 ; 6 ; 3 }  +

   +  { 6 ;- 4 ; 2 } = { 12 ; 2 ; 5 } ;      3a + 2b = { 12 ; 2 ; 5 } .

3) A( 1 ; 3 ;- 2 )  i  B( 3 ; 4 ; 1 ) ;   вектор АВ  -  ?

    AB = { 3 - 1 ; 4 - 3 ; 1 + 2 } = { 2 ; 1 ; 3 } .

4)  . . . .

    Вектор  d = a + b - c = { 1 ; 2 ; 3 } + {- 1 ; 2 ;- 3 } - { 5 ; 2 ;- 2 } =

    =  { 0 ; 4 ; 0 } - { 5 ; 2 ;- 2 } = {- 5 ; 2 ; 2 } ;      d =  {- 5 ; 2 ; 2 } ;

    | d | = √[ (- 5 )² + 2² + 2² ] = √33 ;      | d | = √33 .

Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.

Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:

Числовой коэффициент k отвечает за наклон графика линейной ф-ции:

Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.

В данном случае k < 0, то есть k — отрицательное число.

Из формулы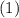 выразим k:

Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:

В итоге, формула линейной функции получится следующей: