Геометрия: Острова, полуострова баренцева моя

Острова, полуострова баренцева моя

Показать ответ

Ответ:

Katenkalovely

09.06.2021 08:07

ответ: а=4 .

ΔАВС - правильный ⇒ все его стороны равны "а" . Высота равностороннего треугольника является и медианой. Так как ОХ⊥ОУ , то если две вершины лежат на оси ОХ, тогда третья вершина лежит на оси ОУ. Пусть вершины А и С лежат на оси ОХ, тогда координаты точки А(х,0) , а координаты точки С(-х,0). Вершина В лежит на оси ОУ и её координаты будут В(0,у) .

По условию сумма всех координат равна:

(-х+0)+(х+0)+(0+у)=2√3 ⇒

у=2√3 (2√3>0 ⇒ точка В лежит в верхней полуплоскости) ⇒ высота ВО=h=2√3 .

По теореме Пифагора из прямоугольного ΔАВО имеем: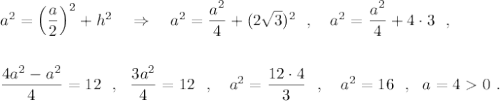 $a^2=\Big(\dfrac{a}{2}\Big)^2+h^2\ \ \ \Rightarrow \ \ \ a^2=\dfrac{a^2}{4}+(2\sqrt3)^2\ \ ,\ \ \ a^2=\dfrac{a^2}{4}+4\cdot 3\ \ ,\\\\\\\dfrac{4a^2-a^2}{4}=12\ \ ,\ \ \dfrac{3a^2}{4}=12\ \ ,\ \ \ a^2=\dfrac{12\cdot 4}{3}\ \ ,\ \ \ a^2=16\ \ ,\ \ a=40\ .$

Длина сторона правильного треугольника равна 4 .

РЕБЯТА две вершины правильного треугольника лежат на оси абцисс, а третья - на оси ординат. Найдите

0,0(0 оценок)

Ответ:

fjfckfk

21.07.2021 02:29

1Соседствующие стороны, имеющие общую границу (точку соприкосновения). Поэтому в данном случае - это стороны, образующие угол, вершина коего и будет их "межа" - точка разделения и соединения одновременно.

2Прямоугольник — четырёхугольник, у которого все углы прямые (равны 90 градусам). В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует. ...

3Прямоугольник — четырёхугольник, у которого все углы прямые (равны 90 градусам). В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует. ...

0,0(0 оценок)

Популярные вопросы: Геометрия