Отрезки AD и CD пересекаются в точке О и делятся этой точкой пополам. На отрезке АС отмечены точки М а на отрезке ВD точка К так что АМ =ВК. Докажите что 1)ОМ=ОК 2) точки М и О и К лежат на одной прямой с рисунком )

ответ: 27 кв см

Условие задачи:

Периметр правильного треугольника, вписанного в окружность, равен 27 см. Найдите периметр и площадь правильного четырехугольника, описанного около этой же окружности.

Объяснение:

Найдем для начала, радиус вписанной окружности.

S=p*r, где  полупериметр р=27/2= 13,5 см, а радиус r - нужно найти.

У правильного треугольника все стороны равны между собой  а углы равны 60° . Так что медиана, КР является и биссектрисой и высотой. Любая  сторона равна 27/3 = 9 см, следовательно из треугольника КРН

по определению косинуса

Отсюда  КР = КН* cos 30 =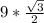

Значит площадь треугольника равна

Значит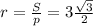

Из рисунка очевидно, что сторона квадрата равна диаметру окружности, то есть

Площадь квадрата равна

кв см

Угловой коэффициент прямой равен: к = Δу/Δх.

к = (-1-(-6))/(-31-(-8)) = 5/(-23).

Он даёт прирост функции на единицу прироста аргумента.

Δу(С) = 5*(-5/23) = -25/23. Это прирост функции от 0 до 5.

Вектор АВ = (-23; 5).

Воспользуемся формулой канонического уравнения прямой:

(x - xa) / (xb - xa)  =   (y - ya) / (yb - ya).  

Подставим в формулу координаты точек:

(x - (-8)) / ((-31) - (-8))  =   (y - (-6)( / ((-1) - (-6)).  

В итоге получено каноническое уравнение прямой:

(x + 8) / (-23)  =   (y + 6) /5.  

Из уравнения прямой в каноническом виде получим уравнение прямой с угловым коэффициентом:

y = (-5 / 23)x - (178 / 23).

Подставим координату х в полученное уравнение.

y = (-5 / 23)*5 - (178 / 23) = -203/23.

ответ: точка С(5; (-203/23).