Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их и
Проведём диагональ в квадрате и диагональ в квадрате
Рассмотрим .
У квадрата все углы прямые.
, по свойству квадрата.
, так как диагонали квадрата делят углы пополам.
по 1 признаку подобия треугольников.
4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
У ромба диагонали взаимно перпендикулярны. Его можно рассматривать, как 2 соединённых треугольника вершинами в разные стороны. Тогда линия, соединяющая 2 соседние стороны ромба - это средняя линия треугольника и она параллельна основанию, то есть диагонали. Аналогично, рассматривая второй треугольник, у него тоже средняя линия параллельна основанию и паралленльна первой линии. Теперь можно перейти к другой диагонали и получит аналогичный результат - линии, соединяющие середины ромба, параллельны между собой и диагоналям. То есть, между ними углы по 90 градусов - это и есть доказательство того, что если последовательно соединить середины сторон ромба, то получится прямоугольник.
Всё в разделе "Объяснение".
Объяснение:1. Неверно.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их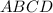
и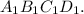 
Проведём диагональ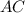
в квадрате 
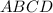и диагональ 
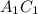в квадрате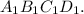 
Рассмотрим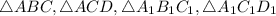
.
У квадрата все углы прямые.4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.Его можно рассматривать, как 2 соединённых треугольника вершинами в разные стороны.
Тогда линия, соединяющая 2 соседние стороны ромба - это средняя линия треугольника и она параллельна основанию, то есть диагонали.
Аналогично, рассматривая второй треугольник, у него тоже средняя линия параллельна основанию и паралленльна первой линии.
Теперь можно перейти к другой диагонали и получит аналогичный результат - линии, соединяющие середины ромба, параллельны между собой и диагоналям.
То есть, между ними углы по 90 градусов - это и есть доказательство того, что если последовательно соединить середины сторон ромба, то получится прямоугольник.