На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH= , FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)
Знак ∪ использован, как знак дуги.
По условию ∪ВС - ∪АС = 40°, а ∪ВС + ∪АС = 180°, так как АВ - диаметр.
∪АС = (180° - 40°)/2 = 70°.
∪ВС = ∪АС + 40° = 110°
∠АВС вписанный, опирается на дугу АС, значит
∠АВС = ∪АС/2 = 70°/2 = 35°.
∠ВАС вписанный, опирается на дугу ВС, значит
∠ВАС = ∪ВС/2 = 110°/2 = 55°
Радиус, проведенный в точку касания, перпендикулярен касательной, поэтому ∠ОАВ = 90°.
∠ОАС = ∠ОАВ - ∠ВАС = 90° - 55° = 35°
Вписанный угол, опирающийся на полуокружность, прямой. Поэтому
∠АСВ = 90°.
∠АСО = ∠АСВ = 90° как смежные.
ΔАОС: ∠АСО = 90°, ∠ОАС = 35°
∠АОС = 90° - 35° = 55° так как сумма острых углов прямоугольного треугольника 90°.
На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH=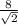 , FH=4√2 см=0,04√2 м
, FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)