1) ДАСВ ~ ДАВС по 1-му признаку подобия прямоугольных треугольников: если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то
|||такие треугольники подобны. А у ДACD и ∆АВС общий острый угол А.
2) Катет AC прямоугольного ДАВС лежит против угла <В = 30°, значит АС равен половине гипотенузы АВ: АС = 0,5AB = 0,5-12 = 6 (см).
Найдём коэффициент подобия АСВ и ДАВС по отношению их гипотенуз AC : AB = 6/12 = 1/2. Следовательно, коэффициент подобия этих треугольников k = 1/2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S(ДАCD) : S(ДАВС) = k² = 1 : 4.
3) Найдём величину катета ВС, используя теорему Пифагора:
BC = √(AB² - AC²) = √(12² - 6²) = √108 = 6√3 (CM)
Известно, что биссектриса угла делит противолежащую сторону на отрезки, пропорциональные прилежащим к углу сторонам. Поэтому СЕ : BE = AC: AB = 1/2.
Тогда СЕ = 1/3 · ВС = 2√3 (см) и ВЕ = 2/3 BC = 4√3 (см)
Запишите уравнение прямой, симметрично прямой y = x - 2 относительно точки A(-3;1)
Объяснение:
Прямая y = x - 2, к=1 ; К(0; -2) принадлежит этой прямой( легко проверяется) .
Пусть уравнение симметричной прямой у₁=к₁х+в₁ .
Т.к прямые симметричные относительно точки, то они параллельны ⇒ их угловые коэффициенты равны , значит к₁=1. Пусть К₁∈у₁ .
Найдем координаты точки К₁(х;у) симметричной точке К( 0;-2) относительно A(-3;1) , по формулам середины отрезка ( тк.АК=АК₁)
х(А)=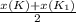
, x(K₁)=-3*2-0=-6,
y(A)=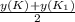
, y((K₁)= 1*2-(-2)= 4 ⇒ K₁(-6; 4 ).
В уравнение у₁=к₁х+в₁ подставим к=1 и K₁(-6; 4 ) , получим 4=1*(-6)+в₁,
в₁=10 . Окончательно получаем у₁=1х+10 или у₁=х+10.
1) ДАСВ ~ ДАВС по 1-му признаку подобия прямоугольных треугольников: если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то
|||такие треугольники подобны. А у ДACD и ∆АВС общий острый угол А.
2) Катет AC прямоугольного ДАВС лежит против угла <В = 30°, значит АС равен половине гипотенузы АВ: АС = 0,5AB = 0,5-12 = 6 (см).
Найдём коэффициент подобия АСВ и ДАВС по отношению их гипотенуз AC : AB = 6/12 = 1/2. Следовательно, коэффициент подобия этих треугольников k = 1/2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S(ДАCD) : S(ДАВС) = k² = 1 : 4.
3) Найдём величину катета ВС, используя теорему Пифагора:
BC = √(AB² - AC²) = √(12² - 6²) = √108 = 6√3 (CM)
Известно, что биссектриса угла делит противолежащую сторону на отрезки, пропорциональные прилежащим к углу сторонам. Поэтому СЕ : BE = AC: AB = 1/2.
Тогда СЕ = 1/3 · ВС = 2√3 (см) и ВЕ = 2/3 BC = 4√3 (см)