1. Периметр соевого сечения конуса равен 360 ед.
2. Объем конуса ед.³
Объяснение:
Требуется найти:
1. Периметр соевого сечения конуса.
2. Объем конуса.
498.
Дано: Конус.
АК = 100; sin∠АКО = 0,6.
Найти: Р (КАМ)
1. Рассмотрим ΔКАО - прямоугольный.
По теореме Пифагора:
КО² = АК² - АО²
КО² = 10000 - 3600 = 6400
КО = 80
⇒ КМ = 80 · 2 = 160
Р (КАМ) = АК + АМ + КМ = 100 + 100 + 160 = 360 (ед.)
504.
Дано: Конус;
r = СО = 2; ∠ВСО = 60°;
Найти: V конуса.
Объем конуса найдем по формуле:
, где r - радиус основания, h - высота конуса.
1. Рассмотрим ΔСВО - прямоугольный.
2. Найдем объем:
(ед.³)
1)Дано: циліндр, АВСD- переріз, ВD-діагональ, R=АО=ОД=6 см, кут ВDА=60 градусів
Знайти: АВ, S abcd
з трикутника ВDА ( кут ВАD= 90 градусів)
tg60= AB/AD AD=AO+OD=12 см
AB=AD tg60
AB=12 * корінь з 3
Осьовим перерізом є прямокутник, отже
S=AB*AD
S=12коренів з 3 * 12=144 корінь з 3 (см2)
2)осьовим перерізом є прямокутник, а прямокутник, у якого діагоналі перпендикулярні - це квадрат, отже висота = 2R=10 см
3) з трикутника АВО ВО=R=5см, К-середина АВ, КО=4см,
з трикутника ВОК (кут ВКО = 90 градусів)
За т.Піфагора ВК= корінь квадратний 25-16= 3 см
АВ=2ВК=6 см
АС=h=8 cм
S= 8*6=48 (cм2)
4) АО=R=5см, KA і КВ - твірні, KA=13 cм , KO-?, Sakb-?
з трикутника КОА (кут КОА=90 градусів)
КО=корінь з 169-25=корінь з 144=12
S=АВ*КО/2 АВ=AO+OB=10
S=10*12/2=60 (см2)
1. Периметр соевого сечения конуса равен 360 ед.
2. Объем конуса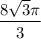 ед.³
ед.³
Объяснение:
Требуется найти:
1. Периметр соевого сечения конуса.
2. Объем конуса.
498.
Дано: Конус.
АК = 100; sin∠АКО = 0,6.
Найти: Р (КАМ)
1. Рассмотрим ΔКАО - прямоугольный.
Синус угла - отношение противолежащего катета к гипотенузе.По теореме Пифагора:
КО² = АК² - АО²
КО² = 10000 - 3600 = 6400
КО = 80
⇒ КМ = 80 · 2 = 160
Р (КАМ) = АК + АМ + КМ = 100 + 100 + 160 = 360 (ед.)
504.
Дано: Конус;
r = СО = 2; ∠ВСО = 60°;
Найти: V конуса.
Объем конуса найдем по формуле:
1. Рассмотрим ΔСВО - прямоугольный.
Тангенс угла - отношение противолежащего катета к прилежащему.2. Найдем объем:
1)Дано: циліндр, АВСD- переріз, ВD-діагональ, R=АО=ОД=6 см, кут ВDА=60 градусів
Знайти: АВ, S abcd
з трикутника ВDА ( кут ВАD= 90 градусів)
tg60= AB/AD AD=AO+OD=12 см
AB=AD tg60
AB=12 * корінь з 3
Осьовим перерізом є прямокутник, отже
S=AB*AD
S=12коренів з 3 * 12=144 корінь з 3 (см2)
2)осьовим перерізом є прямокутник, а прямокутник, у якого діагоналі перпендикулярні - це квадрат, отже висота = 2R=10 см
3) з трикутника АВО ВО=R=5см, К-середина АВ, КО=4см,
з трикутника ВОК (кут ВКО = 90 градусів)
За т.Піфагора ВК= корінь квадратний 25-16= 3 см
АВ=2ВК=6 см
АС=h=8 cм
S= 8*6=48 (cм2)
4) АО=R=5см, KA і КВ - твірні, KA=13 cм , KO-?, Sakb-?
з трикутника КОА (кут КОА=90 градусів)
КО=корінь з 169-25=корінь з 144=12
S=АВ*КО/2 АВ=AO+OB=10
S=10*12/2=60 (см2)