ABCD-трапеция, BC и AD - основания
∠A = 90°, ∠D = 45°, BC = 4см, AB = 18см
BC
| | \
A||___\ D
E
Найти:
S(ABCD) - ?
Дополнительное построение: СЕ⊥AD
∠B = ∠A = ∠C = ∠E = 90° ⇒ ABCE - прямоугольник ⇒ AB = CE = 18см,
BC = AE = 4см
Рассмотрим ΔCED:
∠D = 45°
∠E = 90°
CE = 18 ⇒ ∠C = 90° - ∠D = ∠D = 45° ⇒ ΔCED -р/б ⇒ ED = CE =18см
AD = AE + ED = 4 + 18 = 22см
S(ABCD) = = = 234см²
S(ABCD) = 234см²
P.s: данные на чертёж заносить мне было проблематично, но это необходимо сделать. Мой чертёж чисто схематический, для представления фигуры создан.
3) Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Так как углы, взятые в порядке следования относятся как 1:3:4 , то ∠А=х , ∠В=3х , ∠С=4х и ∠А+∠С=х+4х=5х=180° , х=36° .
∠А=36° , ∠В=3*36°=108° , ∠С=4*36°=144°
Сумма внутренних углов четырёхугольника равна 360°.
∠D=360°-36°-108°-144°=72°
Или ∠В+∠D=5х , ∠D=5x-∠B=3x-3x=2x , 2x=2*36°=72° .
4) Сторона правильного треугольника равна .
Радиус вписанной окружности в прав. тр-к равна 1/3 его высоты, то есть .
Сторона прав.четырёхугольника - квадрата, описанного около окружности, равна .
Периметр квадрата равен см.
ABCD-трапеция, BC и AD - основания
∠A = 90°, ∠D = 45°, BC = 4см, AB = 18см
BC
| | \
A||___\ D
E
Найти:
S(ABCD) - ?
Дополнительное построение: СЕ⊥AD
∠B = ∠A = ∠C = ∠E = 90° ⇒ ABCE - прямоугольник ⇒ AB = CE = 18см,
BC = AE = 4см
Рассмотрим ΔCED:
∠D = 45°
∠E = 90°
CE = 18 ⇒ ∠C = 90° - ∠D = ∠D = 45° ⇒ ΔCED -р/б ⇒ ED = CE =18см
AD = AE + ED = 4 + 18 = 22см
S(ABCD) = = = 234см²
S(ABCD) = 234см²
P.s: данные на чертёж заносить мне было проблематично, но это необходимо сделать. Мой чертёж чисто схематический, для представления фигуры создан.
3) Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Так как углы, взятые в порядке следования относятся как 1:3:4 , то ∠А=х , ∠В=3х , ∠С=4х и ∠А+∠С=х+4х=5х=180° , х=36° .
∠А=36° , ∠В=3*36°=108° , ∠С=4*36°=144°
Сумма внутренних углов четырёхугольника равна 360°.
∠D=360°-36°-108°-144°=72°
Или ∠В+∠D=5х , ∠D=5x-∠B=3x-3x=2x , 2x=2*36°=72° .
4) Сторона правильного треугольника равна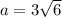 .
.
Радиус вписанной окружности в прав. тр-к равна 1/3 его высоты, то есть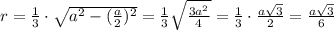 .
.
Сторона прав.четырёхугольника - квадрата, описанного около окружности, равна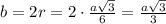 .
.
Периметр квадрата равен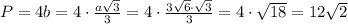 см.
см.