Паралельне перенесення задано формулами х1 = х – 4, у1 = у + 5. Знайдіть координати точки, в яку переходить центр кола (х-3)2 + (у+1)2 = 9​

Пусть дан треугольник АВС с прямым углом А, в котором проведена биссектриса АЕ, длину которой нужно найти.

Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.

Запишем пропорцию:

Пусть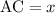 . Тогда .

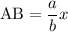Запишем теорему Пифагора для треугольника АВС:

Значит:

Запишем теорему синусов для треугольника АЕС:

Так как АЕ - биссектриса, то ЕАВ и ЕАС равны по половине прямого угла, то есть по 45°.

Синус угла С определим как отношение противолежащего катета к гипотенузе:

Теперь можем найти биссектрису:

ответ: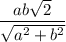

Даны вершины пирамиды А(3,-5,5), В(-5,1,0), С(3,0,5), D(1,-1,4).

1) Находим векторы ВА и ВС.

ВА = (3+5=8; -5-1=-6; 5-0=5) = (8; -6; 5).

Модуль равен √(64+36+25) = √125 = 5√5.

ВС = (3+5=8;0-1=-1; 5-0=5) = (8; -1; 5).

Модуль равен √(64+1+25) = √90 = 3√10.

cos B = (8*8+(-1)*(-6)+5*5)/(5√5*3√10) = 95/(75√2) = 19√2/30 ≈ 0,896.

∠B = arc cos 0,896 = 0,46086 радиан = 26,406 градуса.

2) Площадь треугольника ABС равна половине модуля векторного произведения ВА(8; -6; 5) на ВС(8; -1; 5).

Применим треугольную схему.

i              j             k |             i               j

8            -6           5 |            8             -6

8            -1            5 |            8             -1   =

= -30i + 40j - 8k - 40j + 5i + 48k = -25i + 0j + 40k = (-25; 0; 40).

Модуль равен √(625 + 0 + 1600) = √2225 = 5√89.

Площадь АВС равна (1/2)*5√89 = 5√89/2 ≈ 23,585 кв.ед.

3) Объём пирамиды равен (1/6) смешанного произведения (ВАхВС)*BD.

Находим вектор BD: В(-5,1,0),  D(1,-1,4) = (1+5=6; -1-1=-2; 4-0=4) = (6; -2; 4).

BAxBC = (-25; 0; 40)

V = (1/6)*(-150+0+160) = 10/6 = 5/3 ≈ 1,67 куб.ед.