Щоб знайти відстань від центра кулі до площини трикутника, ми можемо використати теорему Піфагора. Теорема Піфагора говорить, що в прямокутному трикутнику квадрат гіпотенузи рівний сумі квадратів катетів. В нашому випадку, ми знаємо, що радіус кулі складає 5 сантиметрів, і це буде наша гіпотенуза. Також ми знаємо, що сторони трикутника складають 15 сантиметрів і 15 сантиметрів, і це будуть наші катети. Тепер ми можемо розв'язати рівняння, щоб знайти відстань від центра кулі до площини трикутника:
h^2 = 5^2 - (15^2 + 15^2) / 2
h^2 = 25 - 225
h^2 = -200
h =
На жаль, коренем з від'ємного числа не може бути, тому ми можемо сказати, що куля не може дотикатися до всіх сторін трикутника. Щоб куля могла дотикатися до всіх сторін трикутника, радіус кулі повинен бути більшим ніж піввисота трикутника.
Дано: ΔАВС — прямоугольный, окружность (О, ОС), АВ= 12 см, АС = 5 см, О ∈ ВС.
Найти: радиус OD
В прямоугольном треугольнике ΔАВС найдём его гипотенузу по т.Пифагора:
АВ² + АС² = ВС²;
12² + 5² = ВС²;
ВС²= 169;
ВС= 13 см. (Длина стороны не может быть отрицательным числом)
Проведём ОD ⟂ АВ. Треугольники ΔАВС и ΔDBO подобны согласно лемме о подобных треугольниках.
Пусть радиус OC=OD= x. Тогда OB= BC–OC= 13–x.
Поскольку треугольники подобны:
AC/OD= BC/BO;
5/x= 13/(13–x);
5(13–x)= 13x;
65–5x= 13x;
65= 18x;
x= 3 (11/18) см.
ответ: 3 и 11/18 см.
P.S. Рисунок прилагается.
Объяснение:
Щоб знайти відстань від центра кулі до площини трикутника, ми можемо використати теорему Піфагора. Теорема Піфагора говорить, що в прямокутному трикутнику квадрат гіпотенузи рівний сумі квадратів катетів. В нашому випадку, ми знаємо, що радіус кулі складає 5 сантиметрів, і це буде наша гіпотенуза. Також ми знаємо, що сторони трикутника складають 15 сантиметрів і 15 сантиметрів, і це будуть наші катети. Тепер ми можемо розв'язати рівняння, щоб знайти відстань від центра кулі до площини трикутника:
h^2 = 5^2 - (15^2 + 15^2) / 2
h^2 = 25 - 225
h^2 = -200
h =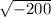
На жаль, коренем з від'ємного числа не може бути, тому ми можемо сказати, що куля не може дотикатися до всіх сторін трикутника. Щоб куля могла дотикатися до всіх сторін трикутника, радіус кулі повинен бути більшим ніж піввисота трикутника.