Пересекаются ли на рисунке: а) отрезки EH и AB, EH и вс, Hк и AB; б) отрезок EH и прямая BC, отре- зок НК и прямая АВ? ответ. а) Отрезки EH и AB А отрезки EH и BC /н б) Отрезок EH и прямая Вс
DC и АВ-основания трапеции ABCD, точка Е-середина стороны ВС. На средней линии трапеции выбрана точка F так, что CDFE-параллелограмм . Известно , что S(ABCD)=38 см² и S(CDFE)=10 см² . Найдите площадь четырехугольника DAEF.
Объяснение:
S(DAEF)=S(DAE)-S(DFE), чертеж 1 . Продолжим часть средней линии трапеции → МЕ.
1) Чертеж 2 ; S(DAE)=S(DЕМ) +S(АЕМ)=
= (опустим высоты Δ DEM, ΔAEM)=
=1/2*МЕ*DP+1/2*ME*AH=1/2*ME*(DP+AH)=( сумма высот
треугольников будет равна высоте трапеции)=1/2*ME*h=
=1/2 * *h=1/2*S(ABCD)=1/2*38=19(cм²).
2)S(DFE)=( диагональ параллелограмма делит его на два
Пусть этот треугольник будет АВС, где АВ и АС это катеты, а ВС - гипотенуза. Так как один угол в прямоугольном треугольнике равен 60, то другой 90-60=30 Значит, что данный треугольник - это половина равностороннего треугольника ДВС (у которого все стороны и углы равны) и меньший катет АС - это будет половина стороны ВС, так как больший катет АВ является одновременно и высотой и медианой равностороннего треугольника ДВС. Тогда пусть катет АС будет х, тогда гипотенуза ВС будет 2х, а их сумму мы знаем и составляем уравнение: х+2х=96 3х=96 х=32 см (это длина катета АС) тогда длина гипотенузы ВС будет 32*2=64 см
DC и АВ-основания трапеции ABCD, точка Е-середина стороны ВС. На средней линии трапеции выбрана точка F так, что CDFE-параллелограмм . Известно , что S(ABCD)=38 см² и S(CDFE)=10 см² . Найдите площадь четырехугольника DAEF.
Объяснение:
S(DAEF)=S(DAE)-S(DFE), чертеж 1 . Продолжим часть средней линии трапеции → МЕ.
1) Чертеж 2 ; S(DAE)=S(DЕМ) +S(АЕМ)=
= (опустим высоты Δ DEM, ΔAEM)=
=1/2*МЕ*DP+1/2*ME*AH=1/2*ME*(DP+AH)=( сумма высот
треугольников будет равна высоте трапеции)=1/2*ME*h=
=1/2 *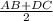 *h=1/2*S(ABCD)=1/2*38=19(cм²).
*h=1/2*S(ABCD)=1/2*38=19(cм²).
2)S(DFE)=( диагональ параллелограмма делит его на два
равновеликих треугольника) = 1/2*S(СDFE)=1/2*10=5 (см²).
S(DAEF)=S(DAE)-S(DFE)=19-5=14 (см²) .
Значит, что данный треугольник - это половина равностороннего треугольника ДВС (у которого все стороны и углы равны) и меньший катет АС - это будет половина стороны ВС, так как больший катет АВ является одновременно и высотой и медианой равностороннего треугольника ДВС. Тогда пусть катет АС будет х, тогда гипотенуза ВС будет 2х, а их сумму мы знаем и составляем уравнение:
х+2х=96
3х=96
х=32 см (это длина катета АС)
тогда длина гипотенузы ВС будет 32*2=64 см