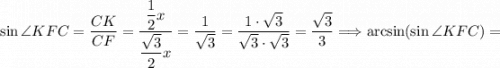Дано: ABCD - тетраэдр, AC = BC = AB = DA = DB = DC, ABK ⊥ CD
Найти: ∠(ABC, ABK) - ?
Решение: Пусть BD = x. Так как по условию AC = BC = AB = DA =
= DB = DC, то x = AC = BC = AB = DA = DB = DC. Проведем из точки K перпендикуляр к прямой AB в точку F. Так как точки A,B ∈ ABC и A,B ∈ ABK, то ABC ∩ ABK = AB.
Так как (F ∈ AB, ABC ∩ ABK= AB ⇒ AB ⊂ ABK) ⇒ F ∈ ABK, то KF ⊂ ABK.
Так как по условию ABK ⊥ CD, то по определению перпендикулярности прямой плоскости, прямая перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости, тогда KF ⊥ CD, так как KF ⊂ ABK. Так как KF ⊥ CD и KF ⊥ AB по построению, то по теореме о трех перпендикулярах CF ⊥ AB.
Так как CF ⊥ AB и KF ⊥ AB, то угол ∠KFC является линейным углом двухгранного угла ∠(ABC, ABK), то есть ∠(ABC, ABK) = ∠KFC.
Так как по условию AC = BC = AB = DA = DB = DC, то тетраэдр ABCD - правильный по определению. По свойствам правильного тетраэдра все его грани правильные треугольники, тогда треугольник ΔABC - правильный. По свойствам правильного треугольника все его углы равны 60°, тогда ∠CAB = 60°. Рассмотрим треугольник ΔCAF. Так как CF ⊥ AB, то треугольник ΔCAF - прямоугольный. . Так как CF ⊥ AB, то CF - высота правильного треугольника ΔABC. По свойствам правильного треугольника все его высоты являются медианами и биссектрисами, тогда точка F - середина отрезка AB. Так как все грани правильного тетраэдра правильные треугольники, то треугольник ΔADB - правильный. Проведем отрезок DF в треугольнике ΔΔADB. Так как точка F - середина отрезка AB, то отрезок DF - медиана, а по свойствам правильного треугольника биссектриса и высота. Так как по свойствам правильного тетраэдра(ABCD) все его грани равны между собой треугольник, то соответствующие элементы треугольников равны, тогда CF = DF как высоты правильных треугольников, следовательно треугольник ΔCFD - равнобедренный с основанием CD. Так как FK ⊥ CD, то по теореме высота равнобедренного треугольника проведенная к основанию(CD) является медианой и биссектрисой, то есть
60°
Объяснение:
Дано: ΔАВС.
АО - медиана, ВН - высота.
АО = ВН.
Найти: ∠ВМО
Продлим АО за точку О на ОК=АО. Из точки К опустим перпендикуляр на продожение АС.
1. Рассмотрим ΔВОК и ΔАОС.
ВО = ОС (условие)
АО = ОК (построение)
Вертикальные углы равны.⇒ ∠1 = ∠2
⇒ ΔВОК = ΔАОС (по двум сторонам и углу между ними. 1 признак)
В равных треугольниках против равных сторон лежат равные углы.⇒ ∠3 = ∠4 -накрест лежащие при ВК и АС и секущей ВС.
⇒ ВК || АС.
2. Рассмотрим НВКР.
ВК || АС (п.1)
Если две прямые перпендикулярны третьей, то они параллельны между собой.⇒ ВН || КР.
При этом ВН ⊥ АР и КР ⊥АР.
⇒ НВКР - прямоугольник.
Противоположные стороны прямоугольника равны.⇒ ВН = КР.
3. Рассмотрим ΔАКР - прямоугольный.
ВН = АО (условие)
ВН = КР (п.2)
⇒ КР = АО
АК = 2АО (построение) ⇒ АК = 2 КР
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ ∠КАР = 30°
4. Рассмотрим ΔАМН - прямоугольный.
Сумма острых углов прямоугольного треугольника равна 90°.⇒ ∠АМН = 90° - ∠КАР = 90° - 30° = 60°
∠АМН = ∠ВМО = 60°
Объяснение:
Дано: ABCD - тетраэдр, AC = BC = AB = DA = DB = DC, ABK ⊥ CD
Найти: ∠(ABC, ABK) - ?
Решение: Пусть BD = x. Так как по условию AC = BC = AB = DA =
= DB = DC, то x = AC = BC = AB = DA = DB = DC. Проведем из точки K перпендикуляр к прямой AB в точку F. Так как точки A,B ∈ ABC и A,B ∈ ABK, то ABC ∩ ABK = AB.
Так как (F ∈ AB, ABC ∩ ABK= AB ⇒ AB ⊂ ABK) ⇒ F ∈ ABK, то KF ⊂ ABK.
Так как по условию ABK ⊥ CD, то по определению перпендикулярности прямой плоскости, прямая перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости, тогда KF ⊥ CD, так как KF ⊂ ABK. Так как KF ⊥ CD и KF ⊥ AB по построению, то по теореме о трех перпендикулярах CF ⊥ AB.
Так как CF ⊥ AB и KF ⊥ AB, то угол ∠KFC является линейным углом двухгранного угла ∠(ABC, ABK), то есть ∠(ABC, ABK) = ∠KFC.
Так как по условию AC = BC = AB = DA = DB = DC, то тетраэдр ABCD - правильный по определению. По свойствам правильного тетраэдра все его грани правильные треугольники, тогда треугольник ΔABC - правильный. По свойствам правильного треугольника все его углы равны 60°, тогда ∠CAB = 60°. Рассмотрим треугольник ΔCAF. Так как CF ⊥ AB, то треугольник ΔCAF - прямоугольный.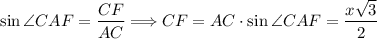 . Так как CF ⊥ AB, то CF - высота правильного треугольника ΔABC. По свойствам правильного треугольника все его высоты являются медианами и биссектрисами, тогда точка F - середина отрезка AB. Так как все грани правильного тетраэдра правильные треугольники, то треугольник ΔADB - правильный. Проведем отрезок DF в треугольнике ΔΔADB. Так как точка F - середина отрезка AB, то отрезок DF - медиана, а по свойствам правильного треугольника биссектриса и высота. Так как по свойствам правильного тетраэдра(ABCD) все его грани равны между собой треугольник, то соответствующие элементы треугольников равны, тогда CF = DF как высоты правильных треугольников, следовательно треугольник ΔCFD - равнобедренный с основанием CD. Так как FK ⊥ CD, то по теореме высота равнобедренного треугольника проведенная к основанию(CD) является медианой и биссектрисой, то есть
. Так как CF ⊥ AB, то CF - высота правильного треугольника ΔABC. По свойствам правильного треугольника все его высоты являются медианами и биссектрисами, тогда точка F - середина отрезка AB. Так как все грани правильного тетраэдра правильные треугольники, то треугольник ΔADB - правильный. Проведем отрезок DF в треугольнике ΔΔADB. Так как точка F - середина отрезка AB, то отрезок DF - медиана, а по свойствам правильного треугольника биссектриса и высота. Так как по свойствам правильного тетраэдра(ABCD) все его грани равны между собой треугольник, то соответствующие элементы треугольников равны, тогда CF = DF как высоты правильных треугольников, следовательно треугольник ΔCFD - равнобедренный с основанием CD. Так как FK ⊥ CD, то по теореме высота равнобедренного треугольника проведенная к основанию(CD) является медианой и биссектрисой, то есть
CK = KD = CD : 2 = x : 2 = 0,5x.
Рассмотрим прямоугольный треугольник ΔCKF.