Периметр рівнобічної трапеції дорівнює 45 см. Знайти середню лінію трапеції, якщо її бічна сторона дорівнює 10 см Кто может скинуть все, пишите в инсту @ar.mi77.7
В обоих случаях площадь ищется по формуле S= 0.5*P*r(r-радиус вписанной окружности) или же для правильного шестиугольника S=3*a*r. Понятно, что при наличии описанного правильного шестиугольника мы ищем площадь сразу через эту формулу, но если мы имеем дело с правильным шестиугольником, вписанным в окружность, то нам необходимо найти радиус вписанной окружности в этом же шестиугольнике. Ищется она по формуле: r=R*cos 180/n, где - количество сторон данного правильного многоугольника. Тогда формула принимает вид r=R*cos 30=R*√3/2
Радиус вписанной окружности правильного многоугольника совпадает с его апофемой (т.е. перпендикуляром, опущенным из центра на любую сторону)
Правильный шестиугольник можно разделить на 6 правильных треугольников. Его площадь равна площади 6 таких треугольников и S(шестиугольника)=6•S (треуг)
Нам известен радиус вписанной в шестиугольник окружности, т.е. высота правильного треугольника АОВ (см. рисунок). Для нахождения площади правильного треугольника воспользуемся формулой
Тогда дм²
––––––––––
2)
По условию
Примем коэффициент отношения радиусов окружностей равным а. Тогда радиус первой равен 5а, второй –3а
5a-3a=40⇒
a=20 см
r1=100 см=1м
S1=π•1²=π м²
60 см=0,6 м
S2=π•(0,6)²=0,36 м²
–––––––––––
3)
Найдите площадь сегмента круга, радиуса 4 см, если его хорда равна 4√2 см
Пусть центр круга О, хорда - АВ.
АО=ВО ⇒∆ АОВ - равнобедренный
По т.косинусов АВ²=АО²+ВО²- 2АО•ВО•cos∠AOB
32=2•16-2•16•cosAOB⇒
cos AOB=0, ⇒ ∠АОВ=90°.
Площадь искомого сегмента равна разности площадей сектора с углом 90° и прямоугольного ∆ АОВ.
Градусная мера полного круга 360°, значит, площадь сектора с углом 90°=1/4 площади круга
S сектора=16π:4=4π
S ∆ АОВ=4•4:2=4•2
S сегм=4π-4•2=4(π-2)= ≈4,566 см²
4)
Отношения отрезков сторон треугольника АВС, на которые их делят данные точки, одинаковы.
Примем коэффициент отношения отрезков сторон равным а.
Тогда АВ=7а.
Треугольники у вершин подобны треугольнику АВС, т.к. имеют общую вершину и стороны исходного треугольника пропорциональны сторонам треугольников, «отсекаемых» от него у вершин, с коэффициентом подобия 7:2, Поэтому эти отсекаемые треугольники равновелики.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Понятно, что при наличии описанного правильного шестиугольника мы ищем площадь сразу через эту формулу, но если мы имеем дело с правильным шестиугольником, вписанным в окружность, то нам необходимо найти радиус вписанной окружности в этом же шестиугольнике.
Ищется она по формуле: r=R*cos 180/n, где - количество сторон данного правильного многоугольника.
Тогда формула принимает вид r=R*cos 30=R*√3/2
1)
Радиус вписанной окружности правильного многоугольника совпадает с его апофемой (т.е. перпендикуляром, опущенным из центра на любую сторону)
Правильный шестиугольник можно разделить на 6 правильных треугольников. Его площадь равна площади 6 таких треугольников и S(шестиугольника)=6•S (треуг)
Нам известен радиус вписанной в шестиугольник окружности, т.е. высота правильного треугольника АОВ (см. рисунок). Для нахождения площади правильного треугольника воспользуемся формулой
Тогда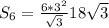 дм²
дм²
––––––––––
2)
По условию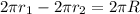
Примем коэффициент отношения радиусов окружностей равным а. Тогда радиус первой равен 5а, второй –3а
5a-3a=40⇒
a=20 см
r1=100 см=1м
S1=π•1²=π м²
60 см=0,6 м
S2=π•(0,6)²=0,36 м²
–––––––––––
3)
Найдите площадь сегмента круга, радиуса 4 см, если его хорда равна 4√2 см
Пусть центр круга О, хорда - АВ.
АО=ВО ⇒∆ АОВ - равнобедренный
По т.косинусов АВ²=АО²+ВО²- 2АО•ВО•cos∠AOB
32=2•16-2•16•cosAOB⇒
cos AOB=0, ⇒ ∠АОВ=90°.
Площадь искомого сегмента равна разности площадей сектора с углом 90° и прямоугольного ∆ АОВ.
Градусная мера полного круга 360°, значит, площадь сектора с углом 90°=1/4 площади круга
S сектора=16π:4=4π
S ∆ АОВ=4•4:2=4•2
S сегм=4π-4•2=4(π-2)= ≈4,566 см²
4)
Отношения отрезков сторон треугольника АВС, на которые их делят данные точки, одинаковы.
Примем коэффициент отношения отрезков сторон равным а.
Тогда АВ=7а.
Треугольники у вершин подобны треугольнику АВС, т.к. имеют общую вершину и стороны исходного треугольника пропорциональны сторонам треугольников, «отсекаемых» от него у вершин, с коэффициентом подобия 7:2, Поэтому эти отсекаемые треугольники равновелики.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
k=АВ:ВК=7:2 ⇒
S (ABC):S(BKM)=k²= 49/4
245:S(BKM)=49:4⇒
S(Δ BKM)=20
S(ТКМОНР)=245-3•20=185 мм²