Периметр равнобедренного треугольника равен 14,6см.его боковая сторона меньше основания на 2,4см.найдите стороны треугольника?

Показать ответ

Ответ:

ksetitaafrgb

17.11.2020 21:16

обозначим проекции точек а; в; с; d и точки о - точки пересечения диагоналей :

a_(1); b_(1); c_(1); d_(1); o_(1)

рассмотрим прямоугольные трапеции aa_(1)d_(1)d и вв_(1)с_(1)с

пересекаются по прямой оо_(1)

оо_(1)- средняя линия трапеции aa_(1)d_(1)d

оо_(1)- средняя линия трапеции вв_(1)с_(1)с

так как средняя линия трапеции равна полусумме оснований, то

из трапеции aa_(1)d_(1)d:

оо_(1)=(аа_(1)+dd_(1))/2

из трапеции вв_(1)с_(1)с :

оо_(1)=(bb_(1)+cc_(1))/2

приравниваем правые части:

(аа_(1)+dd_(1))/2=(bb_(1)+cc_(1))/2 ⇒ [b]аа_(1)+dd_(1)=bb_(1)+cc_(1)[/b]

0,0(0 оценок)

Ответ:

Mild06

01.06.2020 04:38

ответ:

Что и требовалось доказать!

Объяснение:

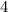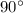Перпендикулярные прямые - прямые, которые пересекаются и при пересечении образуют прямых угла. (углы, градусная мера которых составляет $90^{\circ}$ ).

Допустим, данные прямые перпендикулярны.

Тогда все три угла равны по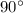 $90^{\circ}$ .

Сумма градусных мер трех неразвернутых углов, образованных при пересечение двух прямых, меньше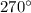 $270^{\circ}$ , по условию.

Проверим: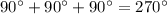 $90^{\circ}+90^{\circ}+90^{\circ}=270^{\circ}$

Исходя из этого, мы доказали, что прямые не перендикулярны, так как сумма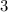 неразвёрнутых углов составляет ровно 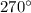$270^{\circ}$ , что не соответствует условию.