Пирамида пересечена плоскостью, параллельной основанию,
которая делит высоту пирамиды в отношении 5 : 7, считая от вершины.
Вычисли площадь основания, если площадь сечения равна 100 дм2.

Х - собственная скорость катера

у - скорость течения

х+у - скорость по течению

х-у - скорость против течения

Составим систему:

6(х+у)=9(х-у)

3(х+у)+5(х-у)=76

6х+6у=9х-9у     (сократим на 3)

3х+3у+5х-5у=76

6х+6у=9х-9у     (сократим на 3)

3х+3у+5х-5у=76

2х+2у=3х-3у

8х-2у=76      (сократим на 2)

2у+3у=3х-2х

4х-у=38

х=5у    (подставим во второе ур-ие)

4*5у-у=38

20у-у=38

19у=38

у=38:19

у=2 (км/ч) скорость течения

х=5у=5*2=10 (км/ч) скорость лодки

ответ: собственная скорость равна 10 км/ч, а скорость течения реки равна 2 км/ч

Объяснение:

Чертеж к решению - во вложении.

Т.к. О - центр вписанной в ΔАВС окружности, то О - точка пересечения биссектрис углов ΔАВС. Значит, АО и ВО - биссектрисы.

Т.к. О1 - центр внеписанной окружности то О1 - точка пересечения биссектрис внешних углов ΔАВС. Значит, АО1 и ВО1 - биссектрисы.

Пусть α - величина внешнего угла ΔАВС при вершине А, тогда (180°-α) - величина внутреннего угла ΔАВС при вершине А, т.к. эти углы - смежные.

Тогда

Аналогично,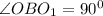

Рассмотрим четырехугольник АОВО1.

У него сумма противолежащих углов А и В равна 90°+90° = 180°.

Т.к. сумма всех углов этого выпуклого четырехугольника равна 360°, то сумма двух других противолежащих при вершинах О и О1 также равна 180°.

Таким образом, воспользуемся утверждением: если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Делаем вывод, точки А, В, О и О1 лежат на одной окружности.

Доказано.